Lesson 1: 数値微分

Lesson 1-1: 有限差分法と前進差分

数値微分に入る前に、微分の数学的な定義を振り返りましょう。関数 \(f(x)\) の導関数は次のように定義されます。 \[f'(x) = \lim_{{h\rightarrow 0}} \frac{f(x+h) - f(x)}{h}.\]

この式を基に、十分に小さな \(h\) を使用して関数 \(f(x)\) の導関数 \(f'(x)\) の近似を考えてみましょう。 \[ f'(x) \approx \frac{f(x+h) - f(x)}{h}. \tag{1}\] この \(h\) の有限な幅を用いた導関数の近似は有限差分近似として知られています。具体的には、式 (1) の表現は前進差分公式と呼ばれます。その意義は、次のセクションで議論される中心差分公式と比較することで明らかになります。

差分近似の精度を確認するために、関数 \(f(x) = e^x\) の \(x=1\) における導関数を式 (1) を使用して評価し、その値を厳密な値 \(f'(1) = e^1 = e\) と比較してみましょう。サンプルのソースコードは以下に示されています。

(lesson1_1.jl)

x = 1.0
h = 0.1
# evaluate the error
f0 = exp(x)
fp = exp(x+h)

dfdx = (fp-f0)/h
error = dfdx-exp(1.0)

println("h=", h)
println("dfdx=",dfdx)
println("Error=", error)

コードの概要：

1. x = 1.0: \( x \) を 1.0 に設定します。
2. h = 0.1: ステップサイズ \( h \) を 0.1 に設定します。
3. f0 = exp(x): \( x = 1.0 \) での \( e^x \) を計算します。
4. fp = exp(x+h): \( x = 1.0 + h \) での \( e^{(x+h)} \) を計算します。
5. dfdx = (fp-f0)/h: 有限差分を使用して \( \frac{df}{dx} \) を近似します。
6. error = dfdx-exp(1.0): 近似と真の導関数 (\( x = 1.0 \) で) の誤差を計算します。
7. println("h=", h): ステップサイズ (\( h \)) を表示します。
8. println("dfdx=",dfdx): 数値微分 (\( \frac{df}{dx} \)) を表示します。
9. println("Error=", error): 誤差を表示します。

Lesson 1-2: 有限差分式の精度と中心差分の近似

前のセクションでの有限差分近似の式は、幅 \(h\) が減少するにつれて誤差も減少することを示しています。誤差の大きさは、次のようにテイラー展開を使用して推定できます： \[f(x+h) = f(x) + f'(x)h + \mathcal{O}(h^2).\] したがって、 \[f'(x) = \frac{f(x+h) - f(x)}{h} + \mathcal{O}(h).\] 前方差分式の誤差は \(\mathcal{O}(h)\) であり、\(h\) が小さい極限では \(h\) に比例します。

ところで、次の2つのテイラー展開を考えてみましょう。 \[ f(x+h) = f(x) + f'(x)h + \frac{1}{2}f''(x)h^2 + \mathcal{O}(h^3),\] \[ f(x-h) = f(x) - f'(x)h + \frac{1}{2}f''(x)h^2 + \mathcal{O}(h^3).\] これらの2つの式の差を取ることで、次の有限差分式を得ることができます。 \[f'(x) = \frac{f(x+h) - f(x-h)}{h} + \mathcal{O}(h^2).\] この有限差分式は 中心差分式 と呼ばれ、正および負の方向で対称に差を取ります。誤差項は \(\mathcal{O}(h^2)\) であり、誤差は \(h^2\) のオーダーです。

実際のプログラムを実装して、ステップサイズ \(h\) に関する前方差分式と中心差分式の精度の挙動を探りましょう。前の例と同様に、以下に関数 \(f(x) = e^x\) の導関数値を計算するプログラムが提供されています。

(lesson1_2.jl)

using PyPlot

# Compute the derivative with the forward difference
function fdiff_forward(x, h)
    fx = exp(x)
    fx_ph = exp(x + h)
    dfdx = (fx_ph - fx) / h
    return dfdx
end

# Compute the derivative with the central difference
function fdiff_central(x, h)
    fx_ph = exp(x + h)
    fx_mh = exp(x - h)
    dfdx = (fx_ph - fx_mh) / (2.0 * h)
    return dfdx
end

# set the numerical parameters
x = 1.0
n = 16

# define the arrays
h = zeros(n)
dfdx_f = zeros(n)
dfdx_c = zeros(n)
error_f = zeros(n)
error_c = zeros(n)

for i in 1:n
    h[i] = 0.8 ^ i
    
# evaluate the derivative    
    dfdx_f[i] = fdiff_forward(x, h[i])
    dfdx_c[i] = fdiff_central(x, h[i])
    
# evaluate the error
    error_f[i] = abs.(dfdx_f[i] - exp(x))
    error_c[i] = abs.(dfdx_c[i] - exp(x))
end


#Plot the date
plt.plot(h, error_f, label="Forward difference")
plt.plot(h, error_c, label="Central difference")

plt.xscale("log")
plt.yscale("log")

plt.xlabel("h")
plt.ylabel("Error")
plt.legend()

plt.savefig("error_derivative.png")
plt.show()

提供されたJuliaコードを調べてみましょう。3行目は#で始まるコメント行で、プログラムには影響を与えませんが、コードを読む際の人間の参照として機能します。4行目では、functionステートメントを使用してtdiff_forward(x, h)手続きを定義しています。このfunctionブロックは、9行目でendで閉じられています。このように定義された手続きは、プログラム内で呼び出すことができます。この4行目は、前進差分式を使用して関数の導関数値を計算し、その値を返す関数を定義しています。さらに、12行目から定義される関数は、中心差分式を使用して導関数値を見つける手続きを定義しています。

24行目では、変数hはサイズnのJulia配列として初期化されています。ここで使用されているzeros関数は、配列をそのすべての要素に1を割り当てて初期化します。同様に、dfdx_f、dfdx_c、error_f、およびerror_fも配列として初期化されています。

30行目で始まるforループでは、前述の前進および中心差分手続きを使用して、ステップサイズh[i]を変えながら関数の導関数値が計算されます。

34行と35行では、計算された数値導関数の近似値と正確な偏微分値の差を取ることで誤差が評価されます。

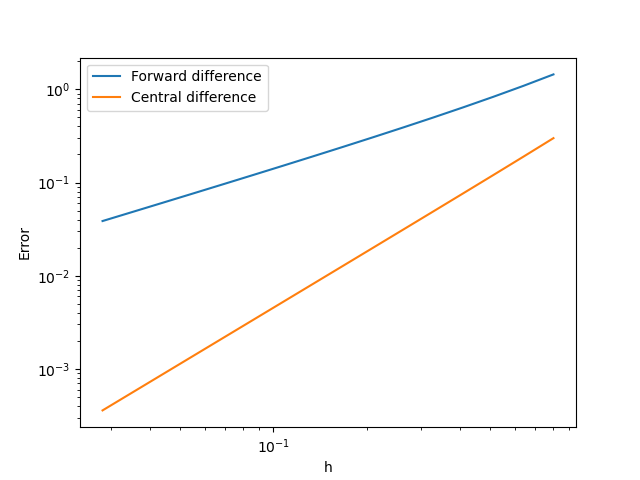
図はこのコードによって生成されるプロットを示しています。特に、図の水平軸と垂直軸は対数スケールです。これを観察すると、前進差分近似の誤差（青い線）と中心差分の誤差（オレンジの線）が\(h\)の異なる冪に比例していることが明らかになります。この挙動は、前述の誤差の大きさに関する議論と一致しています。

Lesson 1-3: 2階微分の数値的な評価

前の節では、有限差分近似を使用して1階微分を数値的に評価しました。この節では、1階微分の数値微分で得られた知識を基にして、数値的に2階微分を評価する方法を学びます。Taylor展開の式を利用することで、次の関係式を導出できます： \[ \frac{f(x+h) - 2f(x) + f(x-h)}{h^2} = \frac{d^2f(x)}{dx^2} + \mathcal{O}(h^2). \] この式は、数値的な二階導関数の評価に使用でき、誤差は\(\mathcal{O}(h^2)\)のオーダーです。

提供されたPythonコードは、関数\(f(x) = \cos(x)\)の数値的な二階導関数\(f''(x)\)を計算するプログラムを示しています。二階導関数とJuliaプログラミングに慣れるために、同様のコードを自分で書いてみてください。

(lesson1_3.jl)

using PyPlot

function second_order_derivative_cos(x, h)
    fx = cos(x)
    fx_ph = cos(x + h)
    fx_mh = cos(x - h)
    d2fdx2 = (fx_ph - 2 * fx + fx_mh) / h^2
    return d2fdx2
end

h = 0.1
nx = 52
xini = 0.0
xfin = 7.0

x = range(xini, stop=xfin, length=nx)
fx = cos.(x)

d2fdx2 = second_order_derivative_cos.(x, h)

plt.plot(x, fx, label="f(x)=cos(x)")
plt.plot(x, d2fdx2, label="f''(x)")

plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.savefig("second_derivative_cos.png")
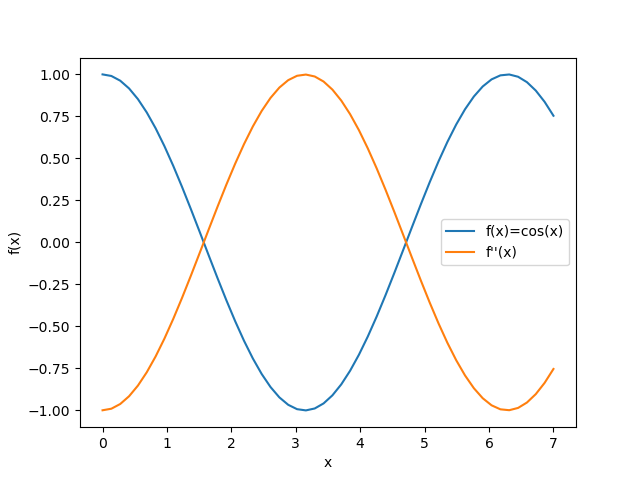
plt.show()

上記のサンプルプログラムは、\( f(x)=(\cos(x) \) および \(f''(x) \) を示す以下の図を提供しています。