Lesson 0: Basics of Python

Lesson 0-1: Execution

First, we will learn the basic steps of Python programming. You can write and execute code in Python by following these steps:

1. Write code in a text editor and save it with the .py extension
2. Execute the prepared .py file using the python command in the terminal.

To learn this process, let's write and execute a simple program called "Hello world." First, write the following Python code and save it as a file named lesson0_1.py.

print('Hello world!!')

Once the above code is ready, enter the following command in the terminal to execute the Python program.

python hello.py

As a result, the following message will be output to the display:

Hello world!!

The print statement used in the above code is a function to output variables. In the case of the above code, the print function is used to output the string Hello world!!. In Python, strings can be treated as character variables by enclosing them in quotation marks ('').

Here, we learned how to write and execute Python code. In the next section, we will learn the basics of Python programming.

Lesson 0-2: Basic Mathematical Operations (Arithmetic and Exponentiation)

In many numerical calculations and analyses, computations are performed by combining basic mathematical operations such as addition, subtraction, multiplication, division, and exponentiation. In this section, we will learn how to perform basic mathematical operations using Python. First, let's take a look at the following sample program.

(lesson0_2.py)

a = 3.0
b = 2.0

print('a=',a)
print('b=',b)

c = a + b
d = a - b
e = a * b
f = a / b
g = a ** b

print('a+b=',c)
print('a-b=',d)
print('a*b=',e)
print('a/b=',f)
print('a**b=',g)

In the program above, the real numbers 3.0 and 2.0 are assigned to variables a and b in the first and second lines, respectively. In Python, the equal sign (=) does not signify that the two sides are equal but represents an instruction to assign the value on the right side to the left side. Next, the instructions in the fourth and fifth lines use the print statement to output the real numbers assigned above.

In Python, addition is represented by the symbol +, subtraction by -, multiplication by *, division by /, and exponentiation by **.

In the code above, the last lines (lines 13 to 17) instruct to output the results of the four arithmetic operations and the exponentiation operation, respectively, using the print statement.

Save the above code in a file with a .py extension and execute it in the terminal using the python command. Doing so will execute the instructions written in the code from top to bottom. Let's check if the results obtained match the expected results.

Lesson 0-3: List

In the source code above, each variable stored a single value. Variables that hold only one value like this are called scalar variables. Scalar variables are the most basic type of variables in programming, but there are many situations where it is useful to store multiple values in a single variable. Here, we will learn about the list, a Python feature prepared for such purposes. First, let's take a look at the following program.

(lesson0_3.py)

la = ['April', 'May', 'June']

print('la=',la)

print('la[0]=',la[0])
print('la[1]=',la[1])
print('la[2]=',la[2])

lb = [1.2, 2.4, 3,6]

print('lb=',lb)

print('lb[0]=',lb[0])
print('lb[1]=',lb[1])
print('lb[2]=',lb[2])

In the first line of the source code above, a list containing the three string elements 'April', 'May', 'June' is created with [] and assigned to the variable la. In Python, lists are created by enclosing elements in [].

In the third line of the source code, the print function is used to output the entire list. In contrast, lines 5-7 output each element of the list one by one. In this way, it is also possible to read only a part of the elements of a list. For example, la[2] represents the second element of the list. However, note that the numbering of elements in a Python list starts from the 0th element.

The explanation above refers to a list with the string elements 'April', 'May', 'June', but variables of other types can also be elements of a list. For example, in lines 10-16 of the source code above, the list lb stores three real numbers, and instructions are shown for outputting each element. Let's run the above Python program to see how lists work.

Lesson 0-4: for Loops (Iteration) and Lists

As we have seen so far, when a program is executed, the computer executes instructions from the beginning of the code in sequence. Therefore, writing programs that require many steps can make the code complex and lengthy. Python provides the for loop as a feature to execute a given instruction repeatedly, helping to write simple and readable code. To learn about for loops, let's first take a look at the following source code.

(lesson0_4.py)

lc = ['April', 'May', 'June']

for l in lc:
    print(l)

print('End')

In the first line of the source code above, a list containing the three strings 'April', 'May', 'June' is created and assigned to the variable lc.

The third line of the code begins defining the area for iteration with the for l in lc: statement. Here, the variable l is a variable whose value changes with each iteration, known as an iterator. In this case, the iterator l holds each element of the list variable lc as its value for each iteration. In the case of the code above, the variable l is assigned the three strings 'April', 'May', 'June' in sequence, and the processing in the iteration area is executed with each repetition.

In Python, the iteration area of a for statement is defined using indentation. Therefore, in the case of the source code above, only the part at line 4, print(l), is repeated.

Once the description of the iteration processing area is completed, remove the indentation to write the next processing content. In the example of the source code above, after the iteration process of the for loop, the indentation is removed, and the program ends by outputting the end log End with print('End').

To summarize the operation of the code above, the program creates a list variable lc with three elements in the first line, uses the for loop to output each element of the list with print(l), and finally outputs the end log ('End') to end the program.

Let's run the above program to see how lists and for loops work for iterative processing.

Lesson 0-5: Range and Iteration

In the previous section, we learned about iterative processing using lists (list). There, we learned how to iterate over each element in a list. In addition to lists, you can perform iterative processing using the range function, which we will learn about here. The range function is a function that generates a sequence of evenly spaced numbers. You can use the sequence generated by this range function to execute a for loop. First, let's look at the following source code to see how the range function works.

(lesson0_5.py)

r = range(5)
print(r)

l = list(r)
print(l)

r2 = range(2,5)
print(r2)

l2 = list(r2)
print(l2)

r3 = range(2,11,2)
print(r3)

l3 = list(r3)
print(l3)

The first line of the source code above demonstrates the simplest use of the range function. When you call the range function in the form of range(n), it generates a sequence of integers from 0 to n-1. In the case of the source code above, range(5) generates the sequence 0,1,2,3,4, and it is stored as a range type object in the variable r.

The fourth line of the source code converts the range type variable r into a list type variable using the list() function. The fifth line then outputs the contents of the converted list to verify the sequence generated by the range function.

In the seventh line of the code, the range function is used in the form of range(n,m). In this case, the range function generates a sequence with the starting point n and the ending point m-1. This sequence can also be converted into a list type object using the list function (list()). In the case of the code example above, the sequence 2,3,4 is generated by range(2,5).

Finally, in the thirteenth line of the code, the range function is used in the form of range(n,m,l). In this case, the range function generates a sequence starting from n, not exceeding m, with a common difference l. In the case of the code above, the sequence 2,4,6,8,10 is generated by range(2,11,2). Let's run the above program to see how the range function works.

Furthermore, as shown in the example of the source code below, you can perform iterative processing using a for loop with the sequence generated by the range function as elements. First, let's take a look at the following source code.

(lesson0_5_for.py)

s = 0
for i in range(1,11):
    s = s + i

print('s=',s)

In the code above, the first line initializes the variable s by assigning it the value 0. The second line starts the definition of the iterative processing area using a for statement with the variable i as the iterator. Here, the range function is used to generate a sequence from 1 to 10, and each integer value of the sequence is assigned to the iterator i for subsequent iterative processing areas.

The third line is indented, indicating that it is within the iterative processing area defined by the for statement. In this line, the value of the iterator i is added to the variable s, and the result is assigned back to s. Finally, in the fifth line, the value of the variable s, calculated through the iterations of the above for loop, is output using a print statement.

Let's think about what processing is being done in the code above and predict the output result. Also, execute the code to check if the expected result is obtained.

Lesson 0-6: If Statements (Conditional Branching)

When writing a program, there may be a need for different processes based on given conditions. In such cases, you can use an if statement to execute different processes for different conditions. To understand the if statement in Python, let's take a look at the following code.

(lesson0_6.py)

a = 2.0
b = 3.0

print("a=", a)
print("b=", b)

if a == b:
    print("a==b")
elif a > b:
    print("a>b")
else:
    print("a<b")

In the code above, the first and second lines assign the real numbers 2.0 and 3.0 to variables a and b, respectively, and lines four and five output their values using the print statement.

Starting from the seventh line, conditional branching is performed with an if statement. An if statement in Python begins with:

if condition:

where condition contains the condition to be evaluated. If this condition is met, the instructions in the indented area (block) below if condition: are executed. In the example code above, the condition a==b is used, and if the values of variables a and b are equal, the indented print("a==b") is executed, and a==b is outputted.

The given condition is not always met. If the condition in if condition: is not met, the indented area below it is skipped, and the process moves to the next condition evaluation. In Python, the following statement is used for the second and subsequent condition evaluations:

elif condition2:

If this condition2 is met, the process in the indented area below it is executed. In the case of the code above, if a is greater than b, print("a>b") is executed, and a>b is outputted.

In Python's conditional branching, an else statement is provided to describe the process for cases that do not match any of the conditions specified in if or elif statements. By writing else: after an if or elif statement, you can specify the process for when none of the previously stated conditions apply. In the case of the code above, if a and b are not equal and a is not greater than b, print("a<b") is executed, and a<b is outputted.

In Python programming, blocks for iterative processing with for statements and conditional branching with if statements are defined by indentation, so there is no need to write an explicit end to the if statement like an end if clause. The end of an if statement is indicated by removing the indentation.

Lesson 0-7: Defining and Calling Functions

When writing programs, there are times when you want to execute the same procedure multiple times. In such cases, by defining a function to perform the necessary procedure and calling that function, you can avoid having to write the same code over and over again. To learn about defining and calling functions, let's take a look at the following source code.

(lesson0_7.py)

def my_func(x):
    y = x*x
    return y


for x in range(11):
    y = my_func(x)
    print(x,y)

In the code above, the first line defines a new function named my_func. In Python, functions can be defined in the following form:

def function_name(argument1, argument2, …):

Here, argument1, argument2, etc., are variables provided from outside to the function for processing within it. The def statement ends with a colon (:), and the processing within the function is written in the indented area starting from the next line.

In the example code, the function reads x as an argument from outside, and on the second line, as part of the function's internal processing, it stores the value of x squared in the variable y.

The last line of the function definition (third line) uses the return statement to indicate that the function's processing is completed and control returns to the caller. At this point, by specifying the return value after the return statement in the form:

return return_value1, return_value2, …

you can return the result of the processing performed within the function back to the caller. In the example code, the third line uses return y to return the value of y, calculated inside the function, back to the caller.

A function defined in this way can be called from within the program. In the example code, starting from the sixth line, the for statement changes the value of x from 0 to 10 while calling the previously defined function my_func. The value returned from the function my_func is stored in the variable y, and then it is output using the print statement.

Let's run the above program to check how function definition and calling work.

Lesson 0-8: Numpy and Matplotlib

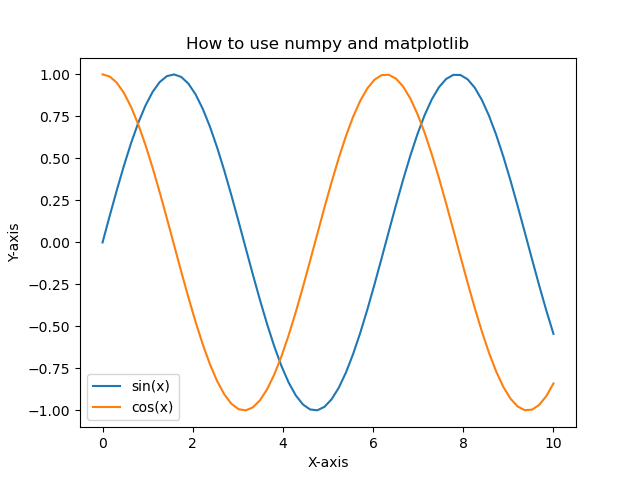
In this section, we will learn how to perform numerical computations and visualize their results using numpy and matplotlib in Python. Numpy is a library for numerical computations, and Matplotlib is a library for visualization. Both libraries are very useful and will be frequently used in future projects, so let's get familiar with how to use them here. First, let's take a look at the following code.

(lesson0_8.py)

import numpy as np
import matplotlib.pyplot as plt

# Generate data
x = np.linspace(0.0, 10.0, 64)
y1 = np.sin(x)
y2 = np.cos(x)

# Create a plot
plt.plot(x, y1, label='sin(x)')
plt.plot(x, y2, label='cos(x)')

# Add labels and title
plt.xlabel("X-axis")
plt.ylabel("Y-axis")
plt.title("How to use numpy and matplotlib")

# Add a legend
plt.legend()

# Save the plot to a file with a more descriptive filename
plt.savefig("plot.png")

# Display the plot
plt.show()

In the first line of the source code above,

import numpy as np

numpy is imported, preparing to use numpy's library. Here, as np defines np as a shorthand for numpy, allowing you to call numpy as np.

In the second line,

import matplotlib.pyplot as plt

The fourth line of the code, # Generate data, is a comment line, and lines starting with a sharp (#) are ignored during program execution. Such comment lines are added to help the understanding of the person writing or reading the program.

On the fifth line, a numpy array x is generated with values of points divided evenly into 64 segments from 0.0 to 10.0.

In lines six and seven, for each element of the numpy array x, the values of the trigonometric functions (\(\sin(x), \cos(x)\)) are calculated using numpy's functions np.sin(x) and np.cos(x), and the results are stored in the numpy arrays y1 and y2.

On the tenth line,

plt.plot(x, y1, label='sin(x)')

the plot function plot of pyplot (shorthand plt) draws a line with the numpy array x as the x-axis values and y1 as the y-axis values. Also, label='sin(x)' specifies sin(x) as the legend for the drawn line. The eleventh line does the same as the tenth, drawing a line with x and y2 as the x-axis and y-axis values, respectively.

Lines fourteen to sixteen specify the labels for the x-axis, the y-axis, and the title of the figure, respectively. Additionally, line nineteen's plt.legend() draws the legends (sin(x), cos(x)).

Line twenty-two's plt.savefig("plot.png") saves the figure drawn up to this point as a png file named "plot.png". Moreover, line twenty-five's plt.show() outputs the same figure on the screen, ending the program.

The figure below shows the graph created by the example Python code using matplotlib.

|Next Page: Numerical Differentiation>

[Back to Python]