この記事は、Fortran Advent Calendar 2023の13日目の記事として書かれています。
【計算速度比較】
Fortran vs Julia vs Python
(ルンゲクッタ法を例に)
このページでは、Fortran, Python, Juliaの計算速度を比較します。世間では、Pythonは遅いという話や、JuliaはFortranと同程度に速いという話をよく目にしますが、言語間の計算速度速度の比較の際に、高度に最適化されたライブラリーを呼んで比較が行われたり、特定の言語で書かれたコードのみを最適化して比較を行ったりなどして、必ずしも多くのユーザーにとって意味のある比較が行われていないように思われます。そこで今回は、1次元調和振動子に対するNewtonの運動方程式をRunge-Kutta法を用いて解くという比較的単純な問題に対して、Fortran, Python, Juliaの簡単なコード書いてそれらの計算速度の比較を行います。異なる言語の計算速度比較を公平に比較するために、特に最適化を行わない素朴なコード(大学の授業で数値計算を学び始めたばかりの平均的な学生が書くようなコードを想定)を用いて検証を行います。
1. 問題設定: 1次元調和振動子に対するNewtonの運動方程式
Fortran, Python, Juliaの計算速度を比較するために、ここでは1次元調和振動子のNewton方程式を解くことを考えます。解くべき運動方程式は、 \[m\frac{d^2}{dt^2}x(t)=-k x(t) \tag{1} \] となります。このように、Newtonの運動方程式は2階の常微分方程式です。
数値計算によってNewton方程式の解を求めるために、2階常微分方程式を次のような1階連立微分方程式に書き換えることを考えます。 \[\frac{d}{dt}x(t) = v(t) \tag{2}\] \[\frac{d}{dt}v(t) =-\frac{k}{m}x(t) \tag{3} \] ここで導入された変数\(v(t)\)は速度に他なりません。今回の解析では、式(2)と式(3)の連立微分方程式を初期条件[\(x(0)=0, v(0)=1\)]の下で解きます。また、今回は質量\(m\)とバネ定数\(k\)を共に1に設定して計算を行います。
2. Fortran, Python, Juliaのコード
Fortran, Python, Juliaの計算速度を比較するために、連立した微分方程式, 式(2)と式(3),を4次のRunge-Kutta法を用いて解きます。それぞれの言語を用いて書いたコードを以下に示しました。計算の詳細はそれぞれのコードに目を通してください。大まかなコードの概要として、時間幅dtを0.01に設定し、108ステップの時間発展計算を行っています。また、反復計算の最後の1000ステップの位置\(x(t)\)と速度\(v(t)\)の情報をファイルに書き出しています。
Fortranコード
program main
implicit none
real(8) :: x, v
real(8),allocatable :: xt(:), vt(:)
real(8) :: mass, k, dt
integer :: it, nt
mass = 1d0
k = 1d0
dt = 1d-2
nt = 100000000
allocate(xt(0:nt), vt(0:nt))
x = 0d0
v = 1d0
do it = 0, nt
xt(it) = x
vt(it) = v
call Runge_Kutta_4th(x,v,dt,mass,k)
end do
open(20,file="result_fortran.out")
do it = nt-1000, nt
write(20,"(3e26.16e3)")it*dt, xt(it), vt(it)
end do
close(20)
contains
subroutine Runge_Kutta_4th(x,v,dt,mass,k)
implicit none
real(8),intent(inout) :: x, v
real(8),intent(in) :: dt, mass, k
real(8) :: x1,x2,x3,x4,v1,v2,v3,v4
! RK1
x1 = v
v1 = force(x, mass, k)
! RK2
x2 = v+0.5d0*dt*v1
v2 = force(x+0.5d0*x1*dt, mass, k)
! RK3
x3 = v+0.5d0*dt*v2
v3 = force(x+0.5d0*x2*dt, mass, k)
! RK4
x4 = v+dt*v3
v4 = force(x+x3*dt, mass, k)
x = x + (x1+2d0*x2+2d0*x3+x4)*dt/6d0
v = v + (v1+2d0*v2+2d0*v3+v4)*dt/6d0
end subroutine Runge_Kutta_4th
real(8) function force(x,mass,k)
implicit none
real(8),intent(in) :: x, mass, k
force = -x*k/mass
end function force
end program mainPythonコード
import numpy as np
def Runge_Kutta_4th(x, v, dt, mass, k):
# RK1
x1 = v
v1 = force(x, mass, k)
# RK2
x2 = v + 0.5 * dt * v1
v2 = force(x + 0.5 * x1 * dt, mass, k)
# RK3
x3 = v + 0.5 * dt * v2
v3 = force(x + 0.5 * x2 * dt, mass, k)
# RK4
x4 = v + dt * v3
v4 = force(x + x3 * dt, mass, k)
x = x + (x1 + 2 * x2 + 2 * x3 + x4) * dt / 6
v = v + (v1 + 2 * v2 + 2 * v3 + v4) * dt / 6
return x, v
def force(x, mass, k):
return -x * k / mass
def main():
mass = 1.0
k = 1.0
dt = 1e-2
nt = 100000000
xt = np.zeros(nt + 1)
vt = np.zeros(nt + 1)
x = 0.0
v = 1.0
for it in range(nt + 1):
xt[it] = x
vt[it] = v
x, v = Runge_Kutta_4th(x, v, dt, mass, k)
with open("result_python.out", "w") as f:
for it in range(nt - 1000, nt + 1):
f.write(f"{it * dt:.16e}\t{xt[it]:.16e}\t{vt[it]:.16e}\n")
if __name__ == "__main__":
main()Juliaコード
function main()
mass = 1.0
k = 1.0
dt = 1e-2
nt = 100000000
xt = zeros(Float64, nt+1)
vt = zeros(Float64, nt+1)
x = 0.0
v = 1.0
for it = 1:nt+1
xt[it] = x
vt[it] = v
x, v = Runge_Kutta_4th!(x, v, dt, mass, k)
end
open("result_julia.out", "w") do file
for it = nt-999:nt
println(file, "$(it*dt) $(xt[it]) $(vt[it])")
end
end
end
function Runge_Kutta_4th!(x, v, dt, mass, k)
x1 = v
v1 = force(x, mass, k)
x2 = v + 0.5 * dt * v1
v2 = force(x + 0.5 * x1 * dt, mass, k)
x3 = v + 0.5 * dt * v2
v3 = force(x + 0.5 * x2 * dt, mass, k)
x4 = v + dt * v3
v4 = force(x + x3 * dt, mass, k)
x += (x1 + 2 * x2 + 2 * x3 + x4) * dt / 6
v += (v1 + 2 * v2 + 2 * v3 + v4) * dt / 6
return x, v
end
function force(x, mass, k)
return -x * k / mass
end
main()3. コンパイル、及び計算の実行
今回の比較では、Fortranのコンパイラとしてgfortran (GNU Fortran)とifx (Intel Fortran; 旧ifort)を用います。GNU Fortranは、コンパイル時に計算速度を向上させるための最適化オプションを指定することが出来ますが、今回はO0, O1, O2, 及びO3という4つの最適化オプションについてそれぞれ計算速度を計測することで、コンパイルオプションによる計算速度の影響も調べることにします。また、Intel Fortranの場合は、これらのオプションに加えてxHOSTという実行プロセッサに応じた最適化を行うオプションを追加して検証を行います。
また、Pythonコード(newton.py)はターミナル上でpython newton.pyとして実行し、Juliaコード(newton.jl)についても同様にターミナル上でjulia newton.jlとして実行します。JuliaとFortranの計算速度の比較の際に、Juliaのコンパイル時間について気になる方がいるかもしれませんが、この点については今回の比較結果には影響がないことを確認したので、その点については後述します。
今回用意したFortranコードnewton.f90, Pytohnコードnewton.py, 及びJuliaコードnewton.jlを実行すると、Newton方程式を解いた結果を出力したファイルがそれぞれ出力されます。下図に、3つのコードによって出力された調和振動子の位置\(x(t)\)の時間発展の様子を示しました。3つのコードがともに等しい結果を与えていることが確認できます。
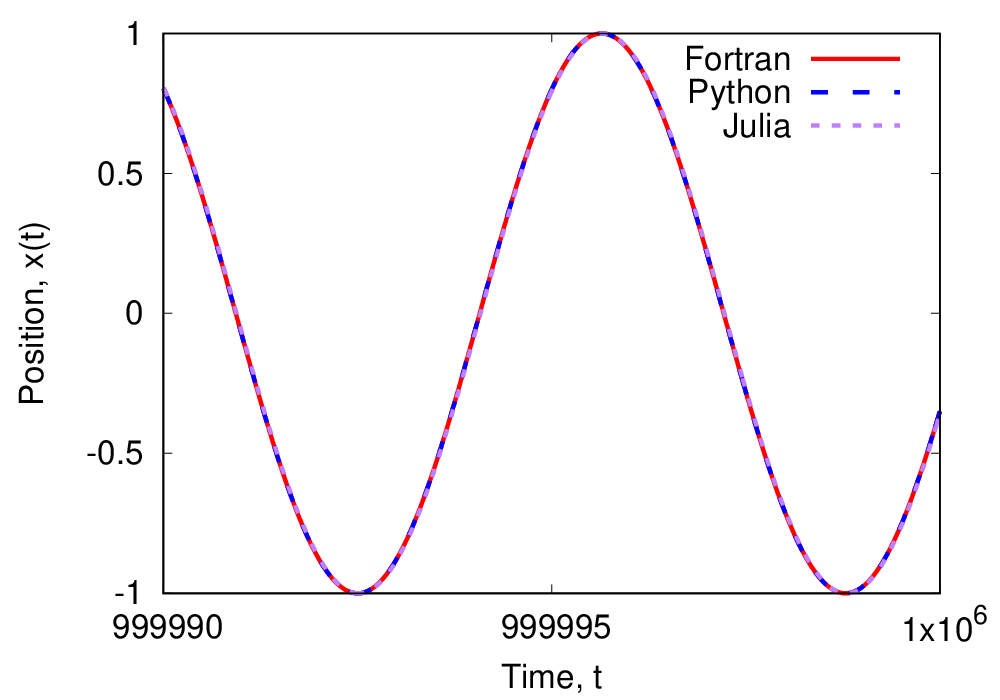
4. Fortran, Python, Juliaの計算速度の比較
Fortran, Python, Juliaの計算速度の比較を行うために、上記の3つの計算コードをそれぞれ5回実行し、各回毎に計算時間の計測を行いました。以下の表に、今回の計測によって得られた実行時間の平均値と標準誤差を示します。
| Newton方程式の求解(108ステップの時間発展)に要する実行時間 | |
|---|---|
| 言語 (コンパイラ名、コンパイルオプション) | 実行時間と標準誤差 |
| Fortran (gfortran -O0) | 3.61 ± 0.00 秒 |
| Fortran (gfortran -O1) | 1.66 ± 0.00 秒 |
| Fortran (gfortran -O2) | 1.69 ± 0.01 秒 |
| Fortran (gfortran -O3) | 1.70 ± 0.02 秒 |
| Fortran (ifx -O0) [旧ifort] | 3.60 ± 0.00 秒 |
| Fortran (ifx -O1) [旧ifort] | 1.16 ± 0.00 秒 |
| Fortran (ifx -O2) [旧ifort] | 1.15 ± 0.00 秒 |
| Fortran (ifx -O3) [旧ifort] | 1.15 ± 0.00 秒 |
| Fortran (ifx -O3 -xHOST) [旧ifort] | 0.92 ± 0.00 秒 |
| Python | 75.33 ± 0.07 秒 |
| Julia | 3.06 ± 0.03 秒 |
上の表で、まずFortranのコンパイラ、及びコンパイルオプションごとの結果を比較してみましょう。今回、比較に用いるFortranコンパイラとして、GNU Fortranコンパイラ (gfortran) とIntel Fortran コンパイラ (ifx; 旧ifort)を採用しています。GNU Fortran コンパイラの場合、最適化を無効化する-O0のオプションを指定すると、最適化が有効になっている他の場合と比べて、実行時間がおよそ2.2倍ほど長くなっています。したがって、Fortranにおいては、最適化が有効化されるとNewton方程式の求解のような計算は2.2倍ほど高速化されることがわかります。また、GNU Fortranの計算結果で、最適化オプションが-O1, -O2, -O3の場合では、実行時間にはほとんど変化がありません。したがって、今回のような単純な計算の場合は、-O1より高度な最適化を行っても、計算速度には良い影響が無いということも分かりました。また、Intel FortranとGNU Fortranの結果を比較すると、最適化を行わない場合(-O0)の実行時間はほぼ一致していますが、-O1以上の最適化を実行すると、Intel Fortranの計算速度がGNU Fortranに比べて優位に速くなります。特に、-O3最適化に加えて-xHOST(プロセッサーに対応した最適化)を行うことで、Intel Fortranの計算速度がGNU Fortranに比べておよそ1.8倍にまで速くなっていることが分かります。
次に、Fortran (ifx -O3 -xHOST)とPythonの実行時間を比較してみると、Fortranの方がPythonと比べて81.9倍ほど速いです。また、Fortran (ifx -O3 -xHOST)とJuliaの実行時間を比較してみると、Fortranの方がJuliaと比べて3.3倍ほど速いです。さらに、JuliaとPythonの実行時間を比較すると、Juliaの方がPythonと比べて24.6倍ほど速いです。

[広告]
 |
 |
 |
5. 速度比較の感想とコメント
上記の比較から、Fortran, Python, Juliaの実行時間を比較すると、Pythonが圧倒的に長い実行時間を要しています。これは、Pythonがインタプリタ型言語であることが原因だと思われます。ただ、これはPythonが劣っているという訳ではなく、豊富なライブラリー環境や書きやすさなどの観点からPythonにはPythonの良さがあり、その良さを反映して現在多くのユーザーに利用されているのだと思います。
また、世間ではJuliaは非常に高速だという話を耳にしますが、実際にFortranと比較してみると3.3倍ほどの実行時間を要していることが分かりました。この3.3倍という数字をどう評価するかは難しいですが、仮に、あなた自身の研究・業務で用いているコードが3.3倍の実行時間が掛かるようになった場合にどう感じるかを想像するとJuliaの善し悪しが見えてくるかもしれません。
6. FortranとJuliaのもう少し真面目な比較
上記の比較では、Juliaコードをjulia newton.jlとして実行して実行時間を計測しているので、コンパイル時間が実行時間に含まれています。したがって、「JuliaとFortranの正確が出来ていない」と感じる人もいるかもしれません。そこで、追加の解析として時間発展のステップ回数を10倍にした計算で実行時間を計測することで、実質的な計算時間を10倍にし、相対的にJuliaのコンパイル時間の影響を抑えた調査を行いました。また、Fortranの方はifx -O3 -xHOSTのコンパイルコマンドを用いて比較を行います。
追加の解析の結果を下の表に示しました。実質的な計算量を10倍にした計算の計測結果を用いてFortranとJuliaの計算速度を比較しても、Fortranの方がJuliaよりも3倍以上速いということが検証できました。
| Newton方程式の求解(109ステップの時間発展)に要する実行時間 | |
|---|---|
| 言語 (コンパイラ名、コンパイルオプション) | 実行時間と標準誤差 |
| Fortran (ifx -O3 -xHOST) | 9.44 ± 0.02 秒 |
| Julia | 29.05 ± 0.00 秒 |
7. Fortranのコンパイル時間に関する調査
上記のセクション【6. FortranとJuliaのもう少し真面目な比較】では、今回の速度比較においてJuliaのコンパイル時間が大きな影響を与えないことを確認しました。それでは、Fortranのコンパイル時間はどうなっているのでしょうか。ここでは、上記のFortranコードのコンパイルにかかる時間を測定します。各コンパイルオプション毎のコンパイル時間の測定結果を以下に示します。
| gfortranのコンパイル時間 | |
|---|---|
| コンパイラ, コンパイルオプション | コンパイル時間 |
| gfortran -O0 | 0.037 秒 |
| gfortran -O1 | 0.039 秒 |
| gfortran -O2 | 0.042 秒 |
| gfortran -O3 | 0.042 秒 |
| ifx -O0 | 0.057 秒 |
| ifx -O1 | 0.066 秒 |
| ifx -O2 | 0.072 秒 |
| ifx -O3 | 0.072 秒 |
| ifx -O3 -xHOST | 0.073 秒 |
8. 比較の実行環境について
今回の検証は、2023年12月28日に以下のような環境で実行しています。
- CPU: Intel(R) Core(TM) i5-1145G7 @ 2.60GHz
- OS: Ubuntu 20.04.6
- GNU Fortran: gfortran version 9.4.0
- Intel Fortran: ifx 2024.0.2 20231213
- Python: Python 3.8.10
- Julia: Julia version 1.7.3