Lesson 3: Numerical Solutions of First-Order Ordinary Differential Equations

Lesson 3-1: Euler Method

Our exploration begins with the basic Euler method. Similar to the discussion on difference methods in Section 1, let us revisit the definition of the derivative. The derivative \(y'(x)\) of the function \(f(x)\) is defined as: \begin{align} y'(x) = \lim_{h\rightarrow 0} \frac{y(x+h) - y(x)}{h}. \tag{2} \end{align} Assuming \(h\) is sufficiently small, the derivative can be approximated using the forward difference formula as follows: \begin{align} y'(x) \approx \frac{y(x+h) - y(x)}{h}. \tag{3} \end{align} Rewriting this equation yields: \begin{align} y(x+h) \approx y(x) + y'(x)h. \tag{4} \end{align}

Looking at equation (4), the right-hand side is expressed using only the information about \(y(x)\) and \(y'(x)\) at \(x\), allowing us to approximately evaluate the function value \(y(x+h)\) at \(x+h\). By repeating this operation, we can evaluate the function value \(y(x)\) at any variable \(x\). This method is known as the Euler method, a numerical solution technique for differential equations. The diagram below visually illustrates the steps of the Euler method.

The following is a more detailed description of the Euler method procedure:

1. First, set the initial condition \(y(x_0) = y_0\) for the differential equation \((1)\).
2. Next, evaluate \(f(x_0, y(x_0))\) to determine the value of the derivative \(y'(x_0)\).
3. Using the evaluated derivative \(y'(x_0)\), compute the value of the function at \(x_0 + h\), \(y(x_0 + h)\), using equation \((4)\).
4. Based on the computed \(y(x_0 + h)\), calculate the function value \(f(x_0 + h, y(x_0 + h))\) and determine the derivative \(y'(x_0 + h)\) at \(x_0 + h\).
5. Using the obtained value of \(y'(x_0 + h)\), evaluate \(y(x_0 + 2h)\) at \(x_0 + 2h\) using equation \((4)\).
6. Repeat the outlined steps below.

By following these steps, it is possible to obtain a numerical solution to the differential equation. As an exercise in solving a spherical differential equation numerically using the Euler method, solve the following differential equation with the initial condition \(y(x=0)=1\):

The analytical solution to this differential equation is the Gaussian function \(y(x)=e^{-x^2}\).

Below is a sample code in C. Write your own code to solve the differential equation and observe how the accuracy of the solution changes as the step size \(h\) varies.

(lesson3_1.c)

#include <stdio.h>

int main() {
    int n, i;
    double x, f, y, y_new, dx, xf;
    FILE *file;

    n = 8;
    xf = 10.0;
    dx = xf / n;

    file = fopen("result_Euler.out", "w");

    x = 0.0;
    y = 1.0 / 10.0;
    fprintf(file, "%16.6e%16.6e\n", x, y);

    for (i = 0; i < n; i++) {
        x = dx * i;
        f = (1.0 - y) * y;
        y_new = y + dx * f;

        x = dx * (i + 1);
        fprintf(file, "%16.6e%16.6e\n", x, y_new);

        y = y_new;
    }

    fclose(file);

    return 0;
}

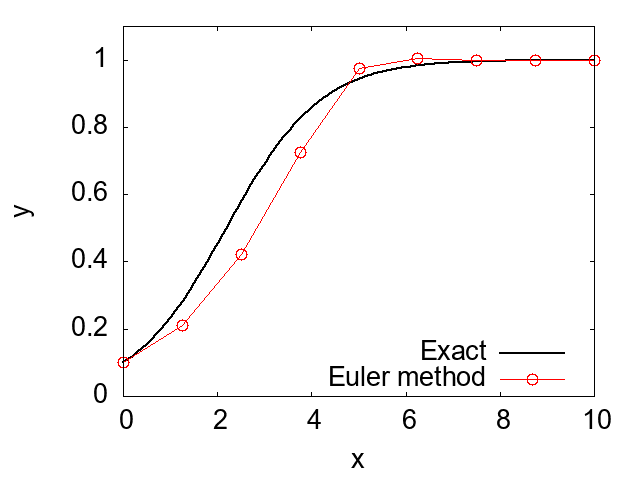
The following figure shows the results obtained from the source code above.

Lesson 3-2: Predictor-Corrector Method

In the previous section, we explored the Euler method as the most basic approach to solving differential equations. However, due to its limitations in accuracy, the Euler method is not commonly used in computational science. This section introduces the predictor-corrector method, which improves accuracy while maintaining simplicity.

\begin{align} \frac{dy\left(x+\frac{h}{2}\right)}{dx} \approx \frac{y(x+h)-y(x)}{h} \tag{6} \end{align}

Furthermore, by performing a transformation similar to the Euler method, we arrive at the following: \begin{align} y(x+h) \approx y(x) + \frac{dy\left(x+\frac{h}{2}\right)}{dx}h. \tag{7} \end{align}

Here, the derivative \( \frac{dy(x+h/2)}{dx} \) is replaced with the average of the derivative values at \(x+h\) and \(x\), using the original differential equation \((1)\) to derive the following relationship: \begin{align} y(x+h) \approx y(x) + h\frac{f\left(x+h, y(x+h)\right) + f\left(x, y(x)\right)}{2}. \tag{8}

In the first step (predictor step), the Euler method is used to obtain an approximate value of \(y(x)\) at \(x+h\): \begin{align} \bar{y}(x+h) = y(x) + hf(x, y(x)). \tag{9}

In the second step (correction step), the approximate value \(\bar{y}(x+h)\) is used to evaluate the right-hand side of equation (7), and \(y(x+h)\) is calculated as follows: \begin{align} y(x+h) = y(x) + h\frac{f\left(x+h, \bar{y}(x+h)\right) + f\left(x, y(x)\right)}{2}. \tag{10}

This two-step procedure for solving differential equations using equations (9) and (10) constitutes the numerical method known as the predictor-corrector method. To compare the accuracy of the predictor-corrector method with the Euler method, we will solve differential equation (5) using the predictor-corrector method and examine the results.

Below is an example of C code for solving differential equation \((5)\) using the predictor-corrector method.

(lesson3_2.c)

#include <stdio.h>

int main() {
    int n, i;
    double x, f, y, y_new, dx, xf;
    double y_pred, f_pred;
    FILE *file;

    n = 8;
    xf = 10.0;
    dx = xf / n;

    file = fopen("result_PredictorCorrector.out", "w");

    x = 0.0;
    y = 1.0 / 10.0;
    fprintf(file, "%16.6e%16.6e\n", x, y);

    for (i = 0; i < n; i++) {
        x = dx * i;
        f = (1.0 - y) * y;
        y_pred = y + dx * f;

        f_pred = (1.0 - y_pred) * y_pred;
        y_new = y + dx * 0.5 * (f + f_pred);

        x = dx * (i + 1);
        fprintf(file, "%16.6e%16.6e\n", x, y_new);

        y = y_new;
    }

    fclose(file);

    return 0;
}

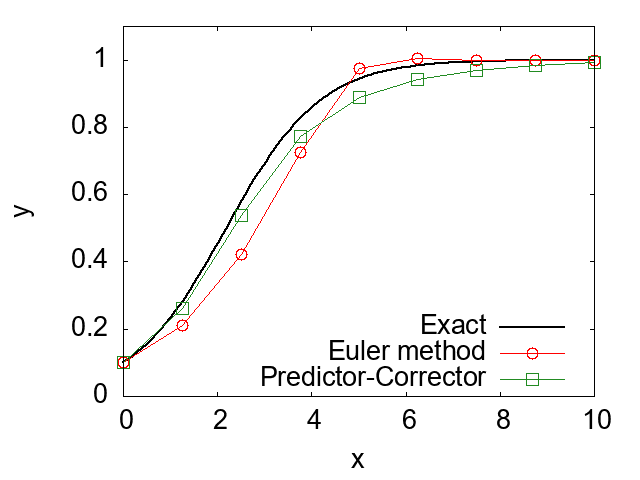
The following figure shows the result obtained using the source code above.