Lesson 4: Numerical Solutions of Second-Order Differential Equations

In this lesson, we will learn how to numerically solve second-order differential equations using the C programming language.

If you use other programming languages, please refer to the following pages:
Solving Second-Order Differential Equations with Python
Solving Second-Order Differential Equations with Julia
Solving Second-Order Differential Equations with Fortran

We will learn how to numerically solve second-order differential equations of the form: \[ \frac{d^2y(x)}{dx^2}=f\left (x,y(x), \frac{dy(x)}{dx} \right). \tag{1} \] Examples of such second-order differential equations include Newton's equation of motion \(m\frac{d^2x(t)}{dt^2}=F(t)\).

There are various methods to solve second-order differential equations. Here, we introduce an auxiliary variable \(s(x)=\frac{dy(x)}{dx}\) and rewrite the equation as a system of two first-order differential equations: \[ \frac{ds(x)}{dx} =f\left (x,y(x), s(x)\right), \tag{2} \] \[ \frac{dy(x)}{dx} =s(x). \tag{3} \]

Solution Using the Euler Method

The following C language source code demonstrates how to solve a system of first-order differential equations using the Euler method.

(lesson4_1.c)

#include <stdio.h>
#include <math.h>

int main() {
    double k, m;
    double x, v, f;
    double x_new, v_new;
    double x_exact, v_exact;
    double t_fin, dt, t;
    int n, i;
    FILE *file;

    n = 20;
    t_fin = 10.0;
    dt = t_fin / n;

    k = 1.0;
    m = 1.0;

    x = 0.0;
    v = 1.0;

    file = fopen("newton_euler.out", "w");

    t = 0.0;
    x_exact = sin(t);
    v_exact = cos(t);

    fprintf(file, "%16.6e%16.6e%16.6e%16.6e%16.6e\n", t, x, v, x_exact, v_exact);

    for (i = 0; i < n; i++) {
        f = -k * x;
        x_new = x + dt * v;
        v_new = v + dt * f / m;

        t = dt * (i + 1);
        x_exact = sin(t);
        v_exact = cos(t);

        fprintf(file, "%16.6e%16.6e%16.6e%16.6e%16.6e\n", t, x_new, v_new, x_exact, v_exact);

        x = x_new;
        v = v_new;
    }

    fclose(file);

    return 0;
}

When this program is executed, a comparison between the numerical solution using Euler's method and the analytical solution is obtained. The figure below shows the results.

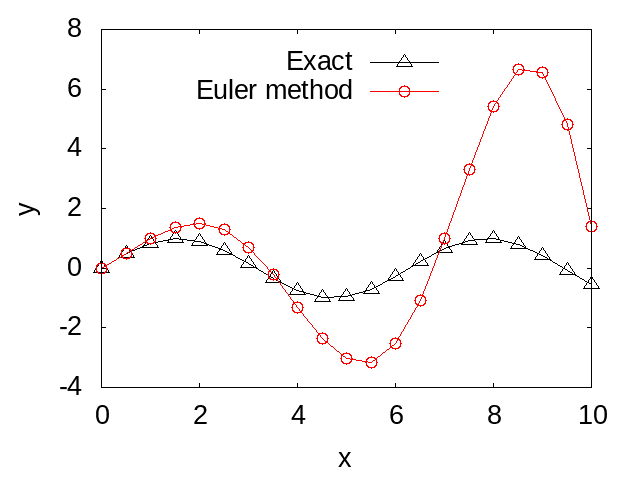
Numerical solution of Newton's differential equation with Euler's method

Predictor-Corrector Method

Next, we will learn how to solve second-order ordinary differential equations using the predictor-corrector method.

(lesson4_2.c)

#include <stdio.h>
#include <math.h>

int main() {
    double k, m;
    double x, v, f;
    double x_pred, v_pred, f_pred;
    double x_new, v_new;
    double x_exact, v_exact;
    double t_fin, dt, t;
    int n, i;
    FILE *file;

    n = 20;
    t_fin = 10.0;
    dt = t_fin / n;

    k = 1.0;
    m = 1.0;

    x = 0.0;
    v = 1.0;

    file = fopen("newton_PredCorr.out", "w");

    t = 0.0;
    x_exact = sin(t);
    v_exact = cos(t);

    fprintf(file, "%16.6e%16.6e%16.6e%16.6e%16.6e\n", t, x, v, x_exact, v_exact);

    for (i = 0; i < n; i++) {
        f = -k * x;
        x_pred = x + dt * v;
        v_pred = v + dt * f / m;
        f_pred = -k * x_pred;

        x_new = x + dt * 0.5 * (v + v_pred);
        v_new = v + dt * 0.5 * (f + f_pred) / m;

        t = dt * (i + 1);
        x_exact = sin(t);
        v_exact = cos(t);

        fprintf(file, "%16.6e%16.6e%16.6e%16.6e%16.6e\n", t, x_new, v_new, x_exact, v_exact);

        x = x_new;
        v = v_new;
    }

    fclose(file);

    return 0;
}

The following figure shows a comparison between the numerical solution obtained and the analytical solution. It can be seen that the predictor-corrector method is more accurate than the Euler method.

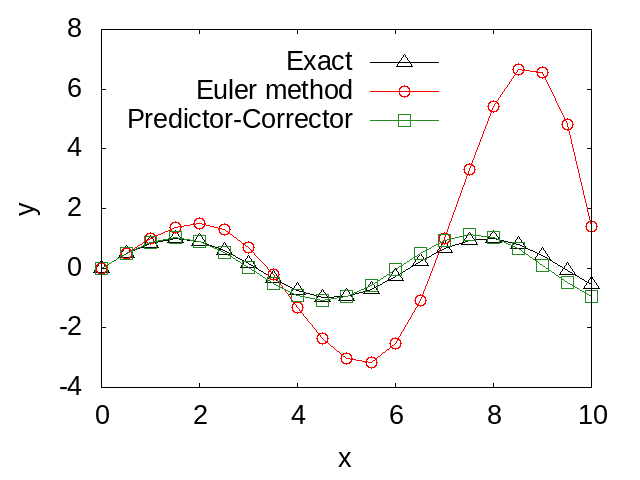
Numerical solution of Newton's differential equation with predictor-corrector method

[Back to C Home]