<Previous Page: Numerical Differentiation|Next Page: Numerical Solutions to First-Order ODEs>
Lesson 2: Numerical Integration
In this page, we will learn about numerical integration, evaluating integrals numerically using the C programming language.
For users of other programming languages, please refer to the following pages:
Numerical Integration with Python
Numerical Integration with Julia
Numerical Integration with Fortran
Lesson 2-1: Trapezoidal Rule and Numerical Integration
To evaluate integrals numerically, let's first review integration. Here, we consider the integration of a function
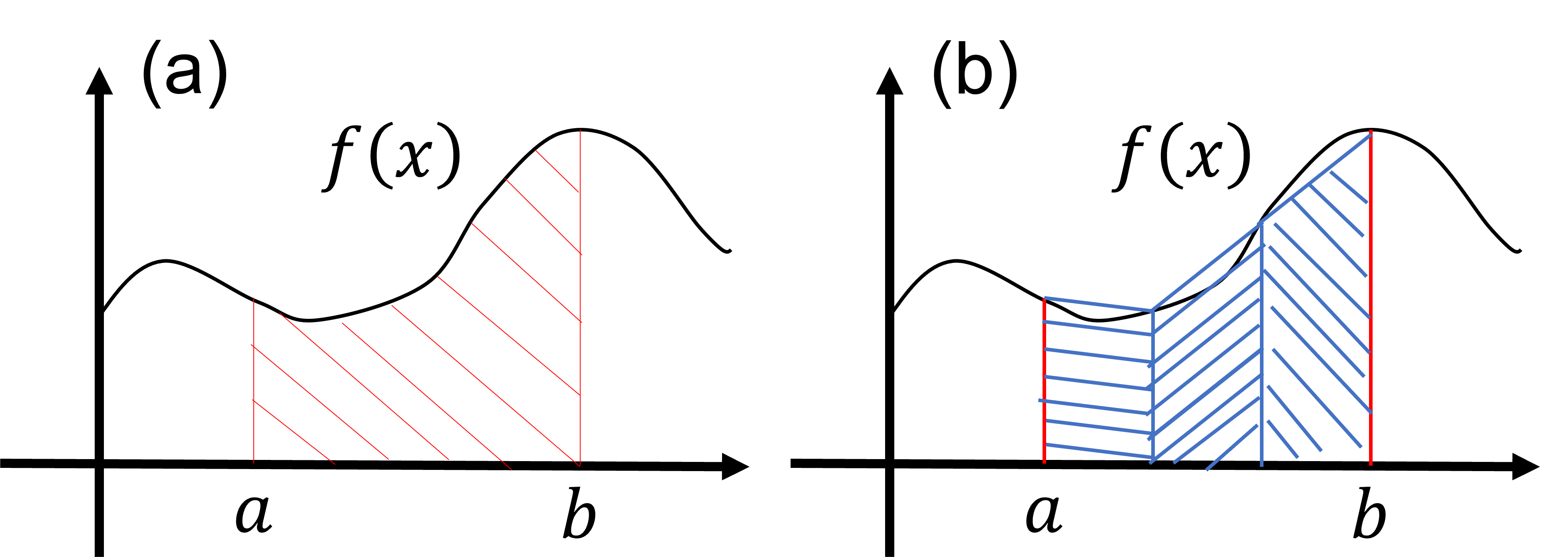
In the above discussion, we considered evaluating the integral in equation (
The approximation formula for integration in equation (
Lesson 2-2: Writing C Language Code Using the Trapezoidal Rule
In this section, we numerically evaluate the following integral using the trapezoidal rule (Equation (
#include <stdio.h> #include <math.h> int main() { int i, n; double a, b; double x, h, f, s; n = 20; a = 0.0; b = 1.0; h = (b - a) / n; x = a; f = 4.0 / (1.0 + x * x); s = 0.5 * h * f; for (i = 1; i < n; i++) { x = a + h * i; f = 4.0 / (1.0 + x * x); s = s + h * f; } x = b; f = 4.0 / (1.0 + x * x); s = s + 0.5 * h * f; printf("Result:\n"); printf("%26.16e\n", s); return 0; }
The above C code performs numerical integration using the trapezoidal rule. Here is an explanation of the code:
- First, the function
fis defined to calculate the value of the functionx. - Next, the function
trapezoidal_ruleis defined, which takes the integration rangenas inputs and evaluates the integral using the trapezoidal rule. - Within the
trapezoidal_rulefunction, the width of each trapezoid is calculated ash. The function computes the average value at the endpoints and then adds the contributions from the interior points to the sum. Finally, the sum is multiplied byhto obtain the approximate value of the integral. - In the
mainfunction, the integration rangenare set, and thetrapezoidal_rulefunction is called to display the result.
Does the result approximate n will yield more accurate results. Try changing the value of n to observe how the error changes.
<Previous page: Numerical Differentiation|Next page: Numerical Solutions of First-Order Ordinary Differential Equations>