Lesson 5: Monte Carlo Method

Lesson 5-1: Example of the Monte Carlo Method: Calculating Pi

In this section, we will learn about the Monte Carlo method. The Monte Carlo method is a mathematical technique that uses random numbers to solve problems and is widely applied in fields such as physics, engineering, and finance.

Below is an example of C language code that applies the Monte Carlo method to estimate the value of pi (π). This method is based on the principle of statistical probability and uses random sampling to derive numerical results.

(lesson5_1.c)

#include <stdio.h>
#include <math.h>

int main() {
    double k, m;
    double x, v, f;
    double x_pred, v_pred, f_pred;
    double x_new, v_new;
    double x_exact, v_exact;
    double t_fin, dt, t;
    int n, i;
    FILE *file;

    n = 20;
    t_fin = 10.0;
    dt = t_fin / n;

    k = 1.0;
    m = 1.0;

    x = 0.0;
    v = 1.0;

    file = fopen("newton_PredCorr.out", "w");

    t = 0.0;
    x_exact = sin(t);
    v_exact = cos(t);

    fprintf(file, "%16.6e%16.6e%16.6e%16.6e%16.6e\n", t, x, v, x_exact, v_exact);

    for (i = 0; i < n; i++) {
        f = -k * x;
        x_pred = x + dt * v;
        v_pred = v + dt * f / m;
        f_pred = -k * x_pred;

        x_new = x + dt * 0.5 * (v + v_pred);
        v_new = v + dt * 0.5 * (f + f_pred) / m;

        t = dt * (i + 1);
        x_exact = sin(t);
        v_exact = cos(t);

        fprintf(file, "%16.6e%16.6e%16.6e%16.6e%16.6e\n", t, x_new, v_new, x_exact, v_exact);

        x = x_new;
        v = v_new;
    }

    fclose(file);

    return 0;
}

The provided C language code estimates the value of π using the Monte Carlo method. This is achieved by generating random points within a unit square and determining the ratio of points that fall inside a unit circle inscribed within the square. Below are the details of the code:

1. #include <stdio.h>, <stdlib.h>, <math.h>, <time.h>: Includes the necessary header files.
2. Variable declarations:
   • isample: A loop variable representing the current iteration of the Monte Carlo simulation.
   • nsample: The number of Monte Carlo samples to be generated (set to 10,000).
   • ncount: A counter to track the number of points within the unit circle.
   • x, y: Variables to store randomly generated values between 0 and 1.
   • r: The Euclidean distance of the point (x, y) from the origin.
3. srand(time(NULL)): Initializes the random number generator.
4. fp = fopen("montecarlo.out", "w"): Opens a file named "montecarlo.out" for writing. This file stores the results of the simulation.
5. for (isample = 1; isample <= nsample; isample++): Begins a loop for the specified number of samples (nsample).
6. x = (double)rand() / RAND_MAX and y = (double)rand() / RAND_MAX: Generates random values x and y, both between 0 and 1.
7. r = sqrt(x * x + y * y): Calculates the Euclidean distance of the point (x, y) from the origin.
8. if (r <= 1.0) ncount++: Checks if the point (x, y) lies within the unit circle (distance from the origin is less than or equal to 1). If true, increments the counter ncount.
9. fprintf(fp, "%10d %10d %26.16e\n", isample, ncount, 4.0 * ncount / (double)isample): Writes formatted output to the file, including the current sample number, the count of points within the unit circle, and the estimated value of π based on the current simulation.
10. fclose(fp): Closes the output file.

In summary, this program performs a Monte Carlo simulation to estimate π by generating random points within a unit square and calculating the proportion of points inside the unit circle. The simulation results are recorded in a file named "montecarlo.out".

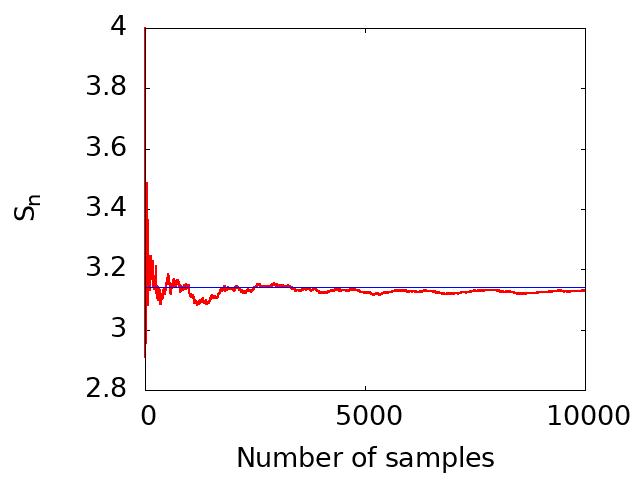
The following diagram visually represents the estimated values of π as a function of the number of sampling points, using the described code. As evident from the graph, the estimated value converges to the true value of π (approximately 3.14) as the number of sampling points increases, illustrating convergence in the limit of large sampling.

Lesson 5-2: Monte Carlo Method for Integration

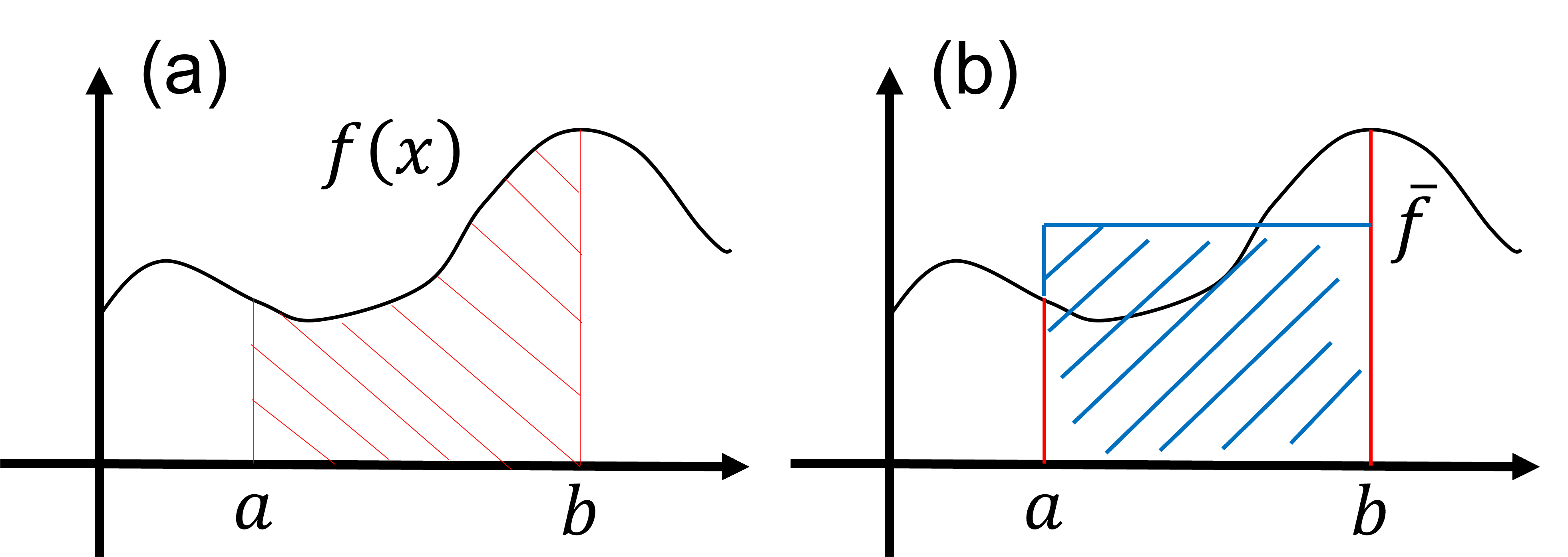
In this lesson, we will explore the Monte Carlo method for integrating functions. Consider the integral: \begin{align} S = \int_a^b dx f(x). \tag{1} \end{align} Here, the value of the integral \(S\) corresponds to the red-shaded area shown in Figure (a). Importantly, this value \(S\) is equivalent to the blue-shaded area depicted in Figure (b). Specifically, it can be expressed as: \begin{align} S = \int_a^b dx f(x) = (b-a) \times \bar{f}, \tag{2} \end{align} where \(\bar{f}\) is the average value of the function \(f(x)\) over the interval \((a \leq x \leq b)\). From this observation, it is suggested that the integral \(S\) can be computed using the average value \(\bar{f}\) of the function \(f(x)\) within the integration range.

The Monte Carlo method for integration involves calculating the average value \( \bar{f} \). In the core algorithm for Monte Carlo integration, to integrate Equation (\(1\)), many random numbers \(x_i\) are generated within the interval \((a \le x \le b)\). Then, the average value \( \bar{f} \) is approximated as: \begin{align} \bar{f} \approx \frac{1}{N} \sum_{i=1}^N f(x_i), \tag{3} \end{align} where \(N\) represents the total number of random numbers generated. Therefore, the integral of Equation (\(1\)) is approximated as: \begin{align} S = \int_a^b dx \, f(x) = (b-a) \times \bar{f} \approx \frac{b-a}{N} \sum_{i=1}^N f(x_i), \tag{4} \end{align} using the set of random numbers \(\{x_i \}\) generated within the interval \((a \le x \le b)\).

To familiarize yourself with the Monte Carlo method, let's develop a C program to evaluate the following integral: \begin{align} S = \int_0^1 dx \frac{4}{1+x^2}. \tag{5} \end{align} When Equation (\(5\)) is analytically integrated, it yields \(S = \pi\).

Below is an example of a C implementation that uses the Monte Carlo method to estimate the value of Equation (\(5\)).

(lesson5_2.c)

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

int main() {
    int isample, nsample;
    double x, f, s;
    FILE *file;

    nsample = 10000;

    s = 0.0;
    file = fopen("pi_montecarlo.out", "w");

    for (isample = 1; isample <= nsample; isample++) {
        x = (double)rand() / RAND_MAX;
        f = 4.0 / (1.0 + x * x);
        s = s + f;
        fprintf(file, "%10d  %26.16e\n", isample, s / isample);
    }

    fclose(file);

    return 0;
}

This C language program executes a Monte Carlo simulation to estimate the value of π. Below are the details of the code:

1. #include <stdio.h>, <stdlib.h>, <time.h>: Includes the necessary header files.
2. Function f(x): Defines the function 4.0 / (1.0 + x * x).
3. Variable declarations:
   • isample: A loop variable representing the current iteration of the Monte Carlo simulation.
   • nsample: The number of Monte Carlo samples generated (set to 10,000).
   • x: A variable to store a randomly generated number between 0 and 1.
   • s: A variable to accumulate the sum of function values.
4. srand(time(NULL)): Initializes the random number generator.
5. fp = fopen("pi_montecarlo.out", "w"): Opens a file named "pi_montecarlo.out" for writing. This file stores the results of the simulation.
6. for (isample = 1; isample <= nsample; isample++): Begins a loop for the specified number of samples (nsample).
7. x = (double)rand() / RAND_MAX: Generates a random number x between 0 and 1.
8. s += f(x): Accumulates the function value based on the randomly generated number x.
9. fprintf(fp, "%10d %26.16e\n", isample, s / isample): Writes formatted output to the file, including the current sample number (isample) and the running average of the accumulated function values, which is used to estimate π.
10. fclose(fp): Closes the output file.

In summary, this program performs a Monte Carlo simulation to estimate the value of π by generating random points and accumulating their contributions to a specific mathematical function. The running average of the accumulated values is used to approximate π, and the results are written to a file named "pi_montecarlo.out".

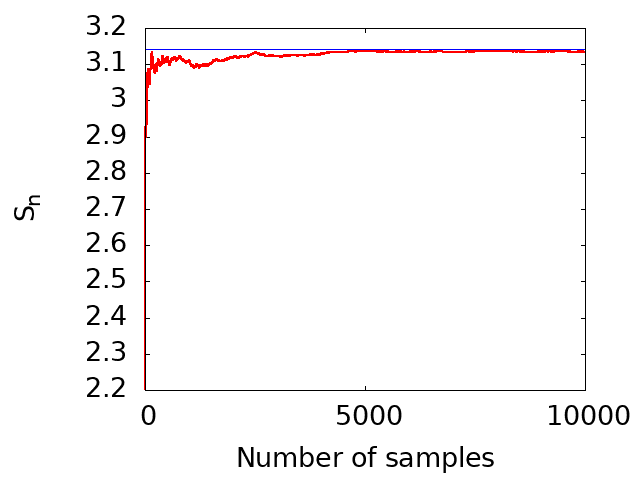
The following figure visually demonstrates the estimated value of π as a function of the number of sampling points using the code (lesson5_2.c). As evident from the figure, the estimated value converges to the true value of π (approximately 3.14) as the number of sampling points increases. Convergence is observed in the limit of large sampling.