Lesson 3: 一階常微分方程式の数値解法

Lesson 3-1: オイラー法

私たちの探索は、基本的なオイラー法から始まります。第1セクションでの差分法の議論と同様に、導関数の定義を再訪しましょう。関数 \(f(x)\) の導関数 \(y'(x)\) は次のように定義されます： \begin{align} y'(x) = \lim_{h\rightarrow 0} \frac{y(x+h) - y(x)}{h}. \tag{2} \end{align} この式で \(h\) が十分に小さいと仮定すると、導関数は次のように前進差分公式を用いて近似できます： \begin{align} y'(x) \approx \frac{y(x+h) - y(x)}{h}. \tag{3} \end{align} この式を書き換えると、次のようになります： \begin{align} y(x+h) \approx y(x) + y'(x)h. \tag{4} \end{align}

式 (4) を見ると、右辺は \(x\) での関数 \(y(x)\) と \(y'(x)\) の情報だけで表されており、関数の値 \(y(x+h)\) を \(x+h\) で近似的に評価できます。このような操作を繰り返すことで、任意の変数 \(x\) での関数の値 \(y(x)\) を評価できます。これは微分方程式の数値解法として知られるオイラー法です。以下の図は、オイラー法の手順を視覚的に示しています。

以下は、オイラー法手順のより詳細な説明です：

1. まず初期条件 \(y(x_0) = y_0\) を微分方程式 \((1)\) に設定します。
2. 次に、\(f(x_0, y(x_0))\) を評価し、導関数の値 \(y'(x_0)\) を求めます。
3. 評価された導関数の値 \(y'(x_0)\) を使用して、式 \((4)\) を用いて \(x_0 + h\) での関数の値 \(y(x_0 + h)\) を計算します。
4. 計算された \(y(x_0 + h)\) を基に、関数の値 \(f(x_0 + h, y(x_0 + h))\) を計算し、導関数の値 \(y'(x_0 + h)\) を \(x_0 + h\) で求めます。
5. 求められた導関数の値 \(y'(x_0 + h)\) を使用して、式 \((4)\) を用いて \(x_0 + 2h\) での関数の値 \(y(x_0 + 2h)\) を評価します。
6. 以下に概説された手順を繰り返します。

これらの手順に従うことで、微分方程式の数値解が可能となります。オイラー法を用いて球状微分方程式を数値的に解く演習として、次の微分方程式を初期条件 \(y(x=0)=1\) で解いてみましょう： \begin{align} y'(x)=-2x y(x). \tag{5} \end{align} なお、この微分方程式の解析解はガウス関数 \(y(x)=e^{-x^2}\) です。

以下はJuliaのサンプルコードです。各自が自分自身のコードを書いて微分方程式を解き、ステップ幅 \(h\) を変えると得られる解の精度がどのように変化するかを観察してみてください。

(lesson3_1.jl)

using PyPlot

# Define the derivative, dy/dx
function dydx(x, y)
    return -2.0 * x * y
end

# Euler method: compute y(x+h)
function euler_method(y, x, h)
    return y + dydx(x, y) * h
end

# Solve the differential equation from x=a to x=b with n discretized points
a = 0.0
b = 2.5
n = 8

h = (b - a) / n
x_values = range(a, stop=b, length=n+1)
y_values = zeros(n+1)
y_exact = zeros(n+1)

# Initial condition, y(a)=y_0
y_values[1] = 1.0
y_exact[1] = 1.0 

for i in 1:n
    y_values[i+1] = euler_method(y_values[i], x_values[i], h)
    y_exact[i+1] = exp(-x_values[i]^2)
end

# Plot the results
plt.plot(x_values, y_values, label="Euler method")
plt.plot(x_values, y_exact, label="Exact solution", linestyle="dashed")

plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.savefig("result_Euler.png")
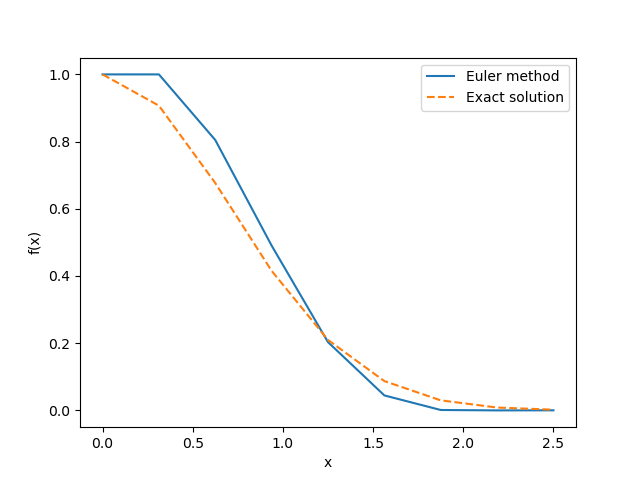
plt.show()

以下の図は、上記のソースコードによって得られた結果を示しています。

Lesson 3-2: 予測子・修正子法

前のセクションでは、微分方程式を解くための最も基本的な手法としてオイラー法を探究しました。しかし、オイラー法はその制度の限界から、計算科学で一般的には使用されません。このセクションでは、制度を向上させつつも単純性を保つ手法、つまり予測子・修正子法を紹介します。

\begin{align} \frac{dy\left(x+\frac{h}{2}\right)}{dx} \approx \frac{y(x+h)-y(x)}{h} \tag{6} \end{align}

更に、オイラー法と同様の変形を行い、以下のようになります。 \begin{align} y(x+h) \approx y(x) + \frac{dy\left(x+\frac{h}{2}\right)}{dx}h. \tag{7} \end{align}

ここでは、導関数 \( \frac{dy(x+h/2)}{dx} \) を \(x+h\) および \(x\) での導関数値の平均に置き換え、元の微分方程式 \((1)\) を利用して、次の関係を導出します。 \begin{align} y(x+h) \approx y(x) + h\frac{f\left(x+h, y(x+h)\right) + f\left(x, y(x)\right)}{2}. \tag{8} \end{align} この式はオイラー法よりも正確な近似を提供しますが、計算上の課題があります。なぜなら、方程式 \((8)\) の右辺を計算する際には \(y(x+h)\) の値が \(x+h\) で必要であり、左辺で \(y(x+h)\) を評価するためです。このため、\(y(x+h)\) の実用的な評価には、式 \((8)\) を用いた2段階の手順が採用されています。

最初に、手順の最初のステップ（予測ステップ）では、オイラー法を使用して \(x+h\) での \(y(x)\) の近似値を取得します： \begin{align} \bar{y}(x+h) = y(x) + hf(x, y(x)). \tag{9} \end{align} ここで、近似値は \(\bar{y}(x+h)\) と表示されます。

その後、手順の第二ステップ（補正ステップ）では、得られた近似値 \(\bar{y}(x+h)\) を利用して、方程式 (7) の右辺を評価し、次のように \(y(x+h)\) を求めます： \begin{align} y(x+h) = y(x) + h\frac{f\left(x+h, \bar{y}(x+h)\right) + f\left(x, y(x)\right)}{2}. \tag{10} \end{align}

方程式 (9) および方程式 (10) を使用して微分方程式を解くこの2段階の手順は、予測修正法として知られる数値解法を構成しています。予測修正法の精度をオイラー法と比較するために、微分方程式 (5) を予測修正法を用いて解き、その結果を比較してみましょう。

以下は、予測修正法を使用して微分方程式 \((5)\) を解く Julia コードの例です。

(lesson3_2.jl)

using PyPlot

# Define the derivative, dy/dx
function dydx(x, y)
    return -2.0 * x * y
end

# Predictor-corrector method: compute y(x+h)
function pred_corr_method(y, x, h)
    y_bar = y + dydx(x, y) * h
    return y + 0.5 * h * (dydx(x, y) + dydx(x + h, y_bar))
end

# Solve the differential equation from x=a to x=b with n discretized points
a = 0.0
b = 2.5
n = 8

h = (b - a) / n
x_values = range(a, stop=b, length=n+1)
y_values = zeros(n+1)
y_exact = zeros(n+1)


# Initial condition, y(a)=y_0
y_values[1] = 1.0
y_exact[1] = 1.0
for i in 1:n
    y_values[i+1] = pred_corr_method(y_values[i], x_values[i], h)
    y_exact[i+1] = exp(-x_values[i+1]^2)
end

# Plot the results
plt.plot(x_values, y_values, label="Predictor-corrector method")
plt.plot(x_values, y_exact, label="Exact solution", linestyle="dashed")

plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.savefig("result_PredCorr.png")
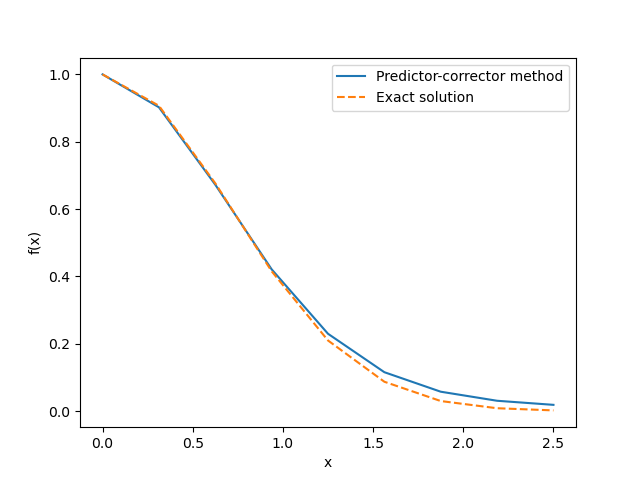
plt.show()

以下の図は、上記のソースコードを使用して得られた結果を示しています。