<前のページへ: 1階常微分方程式の求解数値積分 |次のページへ: モンテカルロ法>
Juliaプログラミング
Lesson 4: 2階常微分方程式の求解
このセクションでは、次の形式で表される2階の常微分方程式の数値解法を探求します: \begin{align} \frac{d^2y(x)}{dx^2} = f\left(x, y(x), \frac{dy(x)}{dx}\right). \tag{1} \end{align} このような方程式の例には、ニュートンの運動方程式 \(m\frac{d^2x(t)}{dt^2} = F(t)\) があります。
2階の常微分方程式を解くためにはさまざまな方法が存在します。ここでは、これらの方程式に対処するために、補助変数 \(s(x) = \frac{dy(x)}{dx}\) を導入します。これにより、方程式 \((1)\) を次の2つの変数についての同時1階常微分方程式の系に変換できます: \[ \frac{ds(x)}{dx} = f\left(x, y(x), s(x)\right), \tag{2} \] \[ \frac{dy(x)}{dx} = s(x). \tag{3} \] この変換により、2階の微分方程式を1階の常微分方程式の系として再定義できます。このアプローチにより、2階の微分方程式の解は、第1階常微分方程式の前のセクションで議論された方法を用いて実現可能となります。
このセクションでは、Juliaを使用して2階の常微分方程式の数値解法を案内します。説明のために、次の2階の常微分方程式を考えます: \begin{align} \frac{d^2x(t)}{dt^2}=-x(t). \tag{4} \end{align} 初期条件は \(x(0)=0, \frac{dx(t)}{dt}=1\) です。
補助変数 \(v(t)=\frac{dx(t)}{dt}\) を導入することで、方程式 (4) は次の同時微分方程式系に再定義されます: \[ \frac{dx(t)}{dt} = v(t), \tag{5} \] \[ \frac{dv(t)}{dt} = -x(t). \tag{6} \] さらに、初期条件 \(x(0)=0, \frac{dx(0)}{dt}=1\) は \(x(0)=0, v(0)=1\) として表現できます。特筆すべきは、この微分方程式の解が \(x(t)=\sin(t)\) および \(v(t)=\cos(t)\) であることです。
提供されたソースコードはJuliaで書かれており、Euler法を用いて同時1階の常微分方程式、式 \((5)\) および \((6)\) を解決するように設計されています。同様の同時微分方程式に対処するための独自のコードを作成する際に、以下の参照コードを考慮してください。
using PyPlot
function dxdt(v)
return v
end
function dvdt(x)
return -x
end
function euler_method(x, v, dt)
x_new = x + dt * dxdt(v)
v_new = v + dt * dvdt(x)
return x_new, v_new
end
tini = 0.0
tfin = 10.0
n = 24
dt = (tfin - tini) / n
time = LinRange(tini, tfin, n + 1)
xt = zeros(n + 1)
vt = zeros(n + 1)
xt_exact = zeros(n + 1)
vt_exact = zeros(n + 1)
# Initial conditions
xt[1] = 0.0
vt[1] = 1.0
xt_exact[1] = 0.0
vt_exact[1] = 1.0
for i in 1:n
xt[i + 1], vt[i + 1] = euler_method(xt[i], vt[i], dt)
xt_exact[i+1]=sin(time[i+1])
vt_exact[i+1]=cos(time[i+1])
end
# Plot the results
plt.plot(time, xt, label="x(t)")
plt.plot(time, vt, label="v(t)")
plt.plot(time, xt_exact, label="x(t): Exact", linestyle="dashed")
plt.plot(time, vt_exact, label="v(t): Exact", linestyle="dashed")
plt.xlabel("t")
plt.ylabel("x,v")
plt.legend()
plt.savefig("diff_2nd_Euler.png")
plt.show()以下の図は、前述のソースコードを実行して得られた数値解と厳密解との比較を示しています。時間 \(t\) が進むにつれて、Euler法によって得られる数値解が厳密解から著しく乖離することが明らかです。
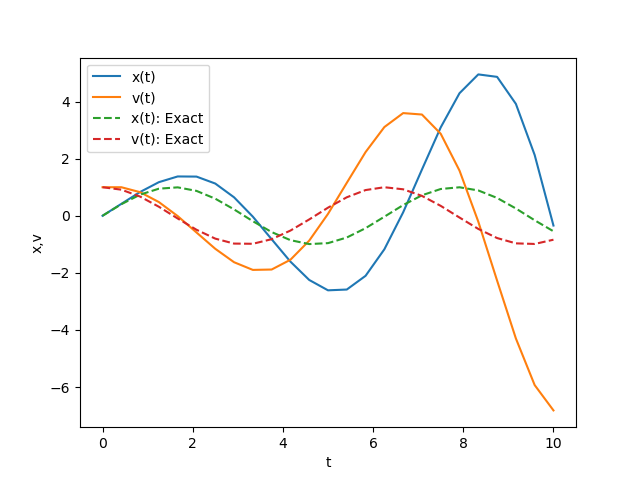
前のセクションでの理解を基に、予測修正法やルンゲ・クッタ法などの手法を使用して数値解の精度を向上させることができます。提供されたサンプルソースコードは、予測修正法を応用して一連の微分方程式、具体的には式 \((5)\) および \((6)\) を解く例を示しています。
using PyPlot
function dxdt(v)
return v
end
function dvdt(x)
return -x
end
function pred_corr_method(x, v, dt)
# Prediction
x_pred = x + dt * dxdt(v)
v_pred = v + dt * dvdt(x)
# Correction
x_new = x + 0.5 * dt * (dxdt(v) + dxdt(v_pred))
v_new = v + 0.5 * dt * (dvdt(x) + dvdt(x_pred))
return x_new, v_new
end
tini = 0.0
tfin = 10.0
n = 24
dt = (tfin - tini) / n
time = LinRange(tini, tfin, n + 1)
xt = zeros(n + 1)
vt = zeros(n + 1)
xt_exact = zeros(n + 1)
vt_exact = zeros(n + 1)
# Initial conditions
xt[1] = 0.0
vt[1] = 1.0
xt_exact[1] = 0.0
vt_exact[1] = 1.0
for i in 1:n
xt[i + 1], vt[i + 1] = pred_corr_method(xt[i], vt[i], dt)
xt_exact[i+1]=sin(time[i+1])
vt_exact[i+1]=cos(time[i+1])
end
# Plot the results
plt.plot(time, xt, label="x(t)")
plt.plot(time, vt, label="v(t)")
plt.plot(time, xt_exact, label="x(t): Exact", linestyle="dashed")
plt.plot(time, vt_exact, label="v(t): Exact", linestyle="dashed")
plt.xlabel("t")
plt.ylabel("x,v")
plt.legend()
plt.savefig("diff_2nd_PredCorr.png")
plt.show()以下の図は、得られた数値解と厳密解との比較を示しています。特に、予測修正法はオイラー法と比較して精度が著しく向上していることが顕著です。
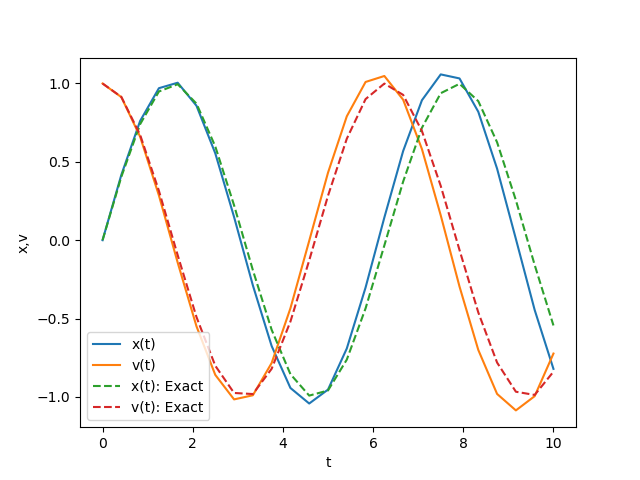
<前のページへ: 1階常微分方程式の求解数値積分 |次のページへ: モンテカルロ法>