Lesson 5-1: モンテカルロ法の例（円周率の計算）

このセクションでは、モンテカルロ法を探求します。モンテカルロ法は、物理学、ファイナンス、エンジニアリングなどでよく遭遇する複雑な問題の解を推定するためにランダムサンプリングを活用する計算アプローチです。この方法は、多くのランダムサンプルを生成し、ランダム変数に影響を受けるプロセスのさまざまな結果の確率をシミュレートして現象をモデル化します。複数のシミュレーションを実行することで、この方法は解析的な解法では複雑すぎる問題に対して統計的な近似値を提供し、シミュレーションの数が増えるにつれて精度が向上します。

以下は、モンテカルロ法を使用して円周率（π）の値を推定するJuliaコードの例です。この方法は統計的確率の原理に基づき、ランダムサンプリングを使用して数値結果を得ることに依存しています。

(lesson5_1.jl)

using PyPlot

# Number of random points to generate
n = 10000

# Initializing counters for points inside and outside the circle
num_inside_circle = 0
num_outside_circle = 0

# Arrays for storing points for plotting
x_inside = Float64[]
y_inside = Float64[]
x_outside = Float64[]
y_outside = Float64[]

# Generating random points and calculating Pi
for _ in 1:n
    x, y = rand(), rand()
    distance = x^2 + y^2

    if distance <= 1
        num_inside_circle += 1
        push!(x_inside, x)
        push!(y_inside, y)
    else
        num_outside_circle += 1
        push!(x_outside, x)
        push!(y_outside, y)
    end
end

# Estimating Pi
pi_estimate = 4 * num_inside_circle / n

# Plotting the points
plt.figure(figsize=(6,6))
plt.scatter(x_inside, y_inside, color="blue", s=1)
plt.scatter(x_outside, y_outside, color="red", s=1)
plt.title("Estimation of Pi using Monte Carlo Method: $(pi_estimate)")
plt.xlabel("X-axis")
plt.ylabel("Y-axis")
plt.savefig("pi_mc.png")
plt.show()

提供されたJuliaコードは、円周率（π）の値を推定するためにモンテカルロ法を使用しています。これは、単位正方形内にランダムな点を生成し、その中に内接する単位円内の点の比率を求めることによって達成されます。以下は、コードの詳細です：

1. using PyPlot: この行は、MatplotlibプロットライブラリへのJuliaインターフェースであるPyPlotライブラリをインポートします。
2. n = 10000: 変数nを10,000に設定し、生成するランダムな点の数を表します。
3. カウンターと配列の初期化：
   1. num_inside_circle = 0およびnum_outside_circle = 0: 単位円内および外の点を追跡するカウンター。
   2. x_inside, y_inside, x_outside,およびy_outside: 後でプロットするために座標を保存する配列。
4. ランダムな点の生成とπの計算：
   1. forループはn回実行され、単位正方形内で(x, y)のランダムな点を生成します（xおよびyは0から1の間）。
   2. 各点の原点からの距離をdistance = x^2 + y^2の式を使用して計算します。
   3. If distanceが1以下であれば、点は単位円内にあり、カウンターが増加し、対応する配列に座標が保存されます。距離が1より大きい場合は、点は単位円外にあり、カウンターが更新されます。
5. πの推定：
   1. 変数pi_estimateは、pi_estimate = 4 * num_inside_circle / nの式を使用して計算されます。
6. 点のプロット：
   1. plt.figure(figsize=(6,6)): 図のサイズを設定します。
   2. scatter関数：単位円内（青）および外（赤）の点の散布図を作成します。
   3. タイトル、x軸のラベル、およびy軸のラベルを設定します。
   4. savefig("pi_mc.png"): プロットを「pi_mc.png」というファイルに保存します。
   5. plt.show(): プロットを表示します。

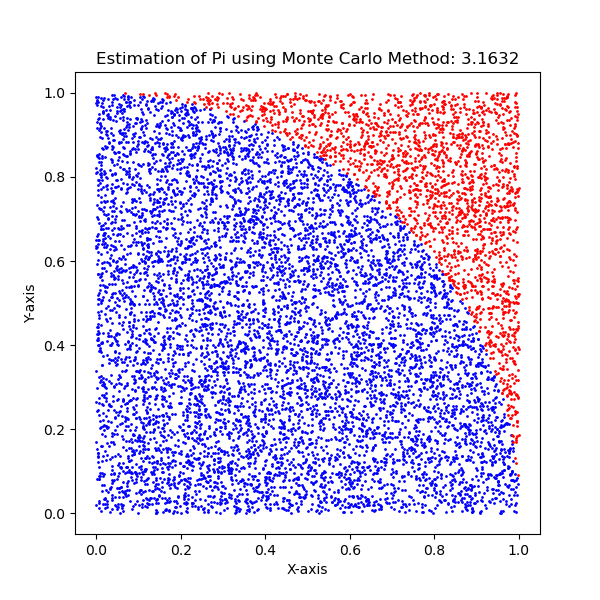
採用されたモンテカルロ法は確率的アプローチであり、ランダムに生成される点の数が増えるにつれて推定の精度が向上します。添付のプロットは、ランダムサンプリングが効果的に単位正方形および単位円の両方の領域をカバーする様子を鮮やかに示しており、モンテカルロ推定の基本的な概念を明示しています。

提供されたJuliaコードは、モンテカルロ法を使用して円周率（Pi）の値を推定しています。これはランダムに点を生成し、それらの配置が単位円内または外にあるかを判定する方法です。このシミュレーションでは、1万点が生成されました。

以下の図は、これらの点の分布を視覚的に表現しており、円内の点を青で、外の点を赤で示しています。この手法は円の面積と正方形の面積の比率を活用して円周率（Pi）の値を近似しています。特筆すべきは、この推定の精度はシミュレーションで使用される点の数が増えるにつれて向上することです。

Lesson 5-2: 積分のためのモンテカルロ法

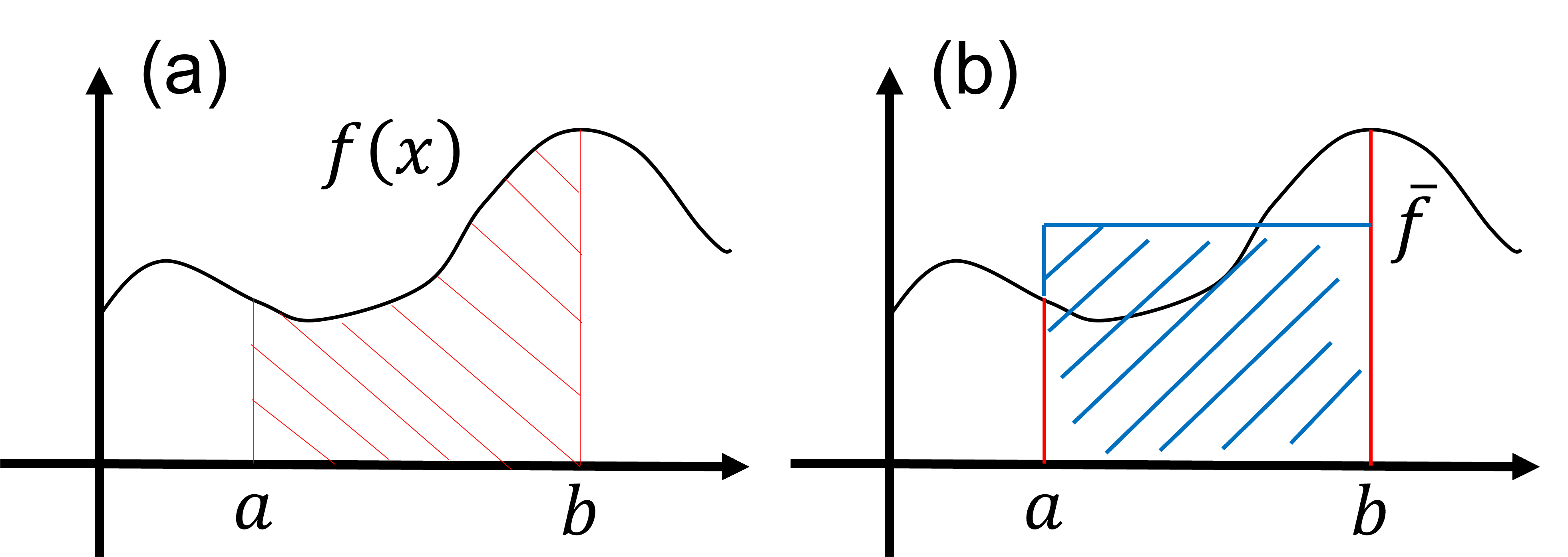
このレッスンでは、関数の積分に対するモンテカルロ法に深く入ります。次の積分を考えてみましょう： \begin{align} S = \int_a^b dx f(x). \tag{1} \end{align} 積分の値 \(S\) は、下記の図(a)で赤で塗りつぶされた領域に対応します。この積分の値 \(S\) は、図(b)で青で示された領域とも等価であり、次のように表されます： \begin{align} S = \int_a^b dx f(x) = (b-a) \times \bar{f}, \tag{2} \end{align} ここで \(\bar{f}\) は区間 \((a \leq x \leq b)\) 上での関数 \(f(x)\) の平均値です。この観察から、積分 \(S\) は積分範囲内での関数 \(f(x)\) の平均値 \(\bar{f}\) を用いて計算できることが示唆されます。

積分のためのモンテカルロ法は、平均値 \( \bar f \) の評価に依存しています。積分式（\(1\)）のモンテカルロ法の基本アルゴリズムでは、区間 \((a \le x \le b)\) 内で多数のランダムな数 \(x_i\) が生成されます。その後、平均値 \( \bar f \) は次のように近似されます： \begin{align} \bar f \approx \frac{1}{N} \sum_{i=1}^N f(x_i), \tag{3} \end{align} ここで \(N\) は生成されたランダムな数の総数を表します。したがって、積分式（\(1\)）の積分は次のように近似されます： \begin{align} S = \int_a^b dx f(x) = (b-a) \times \bar f \approx \frac{b-a}{N} \sum_{i=1}^N f(x_i) \tag{4} \end{align} ここで、範囲 \((a \le x \le b)\) 内で生成されたランダムな数のセット \(\{x_i \}\) を使用しています。

モンテカルロ法に慣れ親しむために、次の積分を評価するためのPythonプログラムを開発してみましょう： \begin{align} S = \int_0^1 dx \frac{4}{1+x^2}. \tag{5} \end{align} 式（\(5\)）を解析的に積分すると、\(S = \pi\) が得られます。

以下のPythonコードは、モンテカルロ法を使用して式（\(5\)）の値 \(S\) を推定する実装の例です。

(lesson5_2.jl)

# Number of random points to use for the Monte Carlo simulation
n = 10000

# Function to integrate
f(x) = 4.0 / (1.0 + x^2)

# Monte Carlo integration
integral = 0.0

for _ in 1:n
    integral += f(rand())
end

integral /= n

println("integral =", integral)

提供されたJuliaコードは、数値積分のためにモンテカルロ法を利用する実例です。各部分とその機能の詳細な解説は以下の通りです：

1. n = 10000: この行は、変数nを10000として初期化し、モンテカルロシミュレーションで使用するランダムな点の数を表します。
2. f(x) = 4.0 / (1.0 + x^2): この行は、関数f(x)を定義しています。この関数は \(f(x)=\frac{4.0}{1.0+x^2} \) の値を計算します。
3. integral = 0.0: この行は、変数integralを0.0で初期化します。この変数はモンテカルロ積分の結果を蓄積します。
4. for _ in 1:n: この行は、n回繰り返すループを開始します。アンダースコア_はループ変数を示すプレースホルダであり、ループ本体では使用されません。
5. integral += f(rand()): ループ内でrand()を使用してランダムな数が生成され、そのランダムな点での関数f(x)の値がintegralに加算されます。
6. integral /= n: ループの後、蓄積された合計はnで割られ、平均値が得られ、これがモンテカルロ積分の結果を表します。
7. println("integral =", integral): 最後に、println関数を使用して積分の値をコンソールに表示します。結果はモンテカルロ法を使用した積分の推定を表すはずです。

まとめると、このコードはモンテカルロ法の実装を提供し、定義された区間内の関数の積分を推定します。具体的には、区間 [0, 1] 上での 4/(1 + x^2) の積分を近似し、これを使用してπの値を推定します。この近似の精度は、使用されるランダムに生成された点の量に依存しています。

レッスン 5-3: 一般的な分布を用いたモンテカルロ法

前のセクションでは、一様分布からのランダムな数を使用したモンテカルロ法を探索しました。このセクションでは、一様分布の代わりに一般的な分布を使用したモンテカルロ法の応用について詳しく調査します。次の積分を考えてみましょう： \[ S = \int^{\infty}_{-\infty}dx f(x) w(x), \tag{6} \] ここで \( w(x) \) はどこでも非負である分布関数です（つまり、任意の \( x \) に対して \( w(x) \ge 0 \)）かつ正規化されています（\( \int^{\infty}_{-\infty} dx w(x) = 1 \)）。分布関数 \( w(x) \) が非負性および正規化の条件を満たす限り、式（6）の積分は、\( w(x) \) に従って分布するランダムな数を使用して次のように評価できます： \[ S = \int^{\infty}_{-\infty}dx f(x) w(x) \approx \frac{1}{N}\sum^{N}_{i=1} f(x_i), \tag{7} \] ここで \( N \) はランダムな数の数であり、\( \{x_i\} \) は確率分布関数 \( w(x) \) に従って生成されたランダムな数です。

Pythonのrandomモジュールは、一様分布、指数分布、正規分布など、さまざまな分布をサポートしています。さらに、メトロポリスサンプリングなどのメソッドを介して、任意の分布からのランダムな数の生成も可能です。

ここでは、一般的な分布をモンテカルロ法に組み込む例を紹介します。具体的には、正規分布を使用して次の積分を計算します： \[ S=\int^{\infty}_{-\infty}dx x^2 \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}=1. \tag{7} \]

以下のJuliaコードは、モンテカルロ法を使用して方程式（7）での値\( S \)を推定する実装の例を示しています。

(lesson5_3.jl)

# Number of random points to use for the Monte Carlo simulation
n = 10000

# Function to integrate
f(x) = x^2

# Monte Carlo integration
integral = 0.0

for _ in 1:n
    integral += f(randn())
end

integral /= n

println("integral =", integral)

Lesson 5-4: 重要性サンプリング

このセクションでは、Monte-Carloサンプリングの収束を向上させるために、被積分関数に適合する分布関数を利用する技術を探求します。積分を次のように変更して考えてみましょう：

\begin{align} S=\int^{\infty}_{-\infty}dx f(x) =\int^{\infty}_{-\infty}dx \frac{f(x)}{w(x)}w(x), \tag{8} \end{align}

ここで、\( w(x) \) は正規化条件 \( \int^{\infty}_{-\infty}dx w(x)= 1 \) を満たし、かつ \( w(x) > 0 \) である分布関数です。レッスン 5-3からの概念を活用して、式（8）の積分をMonte-Carloサンプリングを使用して評価できます。これは、次の近似で示されるように、分布関数 \( w(x) \) に従ってランダムな数をサンプリングすることで行われます：

\begin{align} S = \int^{\infty}_{-\infty}dx \frac{f(x)}{w(x)}w(x) \approx \frac{1}{N}\sum^N_i \frac{f(x_i)}{w(x_i)}, \tag{9} \end{align}

式（9）で示されるように、Monte-Carloサンプリングの収束速度は比率 \(\frac{f(x_i)}{w(x_i)}\) の変動に影響されます。この比率が \(x\) に関係なく一定である場合、単一のMonte-Carloサンプルでも収束した結果が得られる可能性があります。一般的な状況での収束を迅速にするためには、典型的には関数 \(w(x)\) が \(f(x)\) に近いものを選択することが有利です。この類似性により、サンプリング値 \(\frac{f(x_i)}{w(x_i)}\) の変動が最小限に抑えられ、収束が早まります。

基本的に、分布関数 \(w(x)\) が被積分関数 \(f(x)\) が重要な領域を強調する場合、Monte-Carloサンプリングは加速された収束を経験します。このサンプリング効率を向上させるための最適な分布関数の選択戦略は、「重要性サンプリング」として認識されています。