Lesson 5: モンテカルロ法

Lesson 5-1: モンテカルロ法の例: 円周率の計算

この節では、モンテカルロ法について学びます。モンテカルロ法は、ランダムな数(乱数)を用いて問題を解く数理的な手法で、物理学、工学、金融など幅広い分野で応用されています。

以下は、円周率（π）の値を推定するためにモンテカルロ法を適用するC言語のコードの例です。この方法は統計的確率の原理に基づき、ランダムサンプリングを使用して数値結果を導きます。

(lesson5_1.c)

#include <stdio.h>
#include <math.h>

int main() {
    double k, m;
    double x, v, f;
    double x_pred, v_pred, f_pred;
    double x_new, v_new;
    double x_exact, v_exact;
    double t_fin, dt, t;
    int n, i;
    FILE *file;

    n = 20;
    t_fin = 10.0;
    dt = t_fin / n;

    k = 1.0;
    m = 1.0;

    x = 0.0;
    v = 1.0;

    file = fopen("newton_PredCorr.out", "w");

    t = 0.0;
    x_exact = sin(t);
    v_exact = cos(t);

    fprintf(file, "%16.6e%16.6e%16.6e%16.6e%16.6e\n", t, x, v, x_exact, v_exact);

    for (i = 0; i < n; i++) {
        f = -k * x;
        x_pred = x + dt * v;
        v_pred = v + dt * f / m;
        f_pred = -k * x_pred;

        x_new = x + dt * 0.5 * (v + v_pred);
        v_new = v + dt * 0.5 * (f + f_pred) / m;

        t = dt * (i + 1);
        x_exact = sin(t);
        v_exact = cos(t);

        fprintf(file, "%16.6e%16.6e%16.6e%16.6e%16.6e\n", t, x_new, v_new, x_exact, v_exact);

        x = x_new;
        v = v_new;
    }

    fclose(file);

    return 0;
}

提供されたC言語のコードは、モンテカルロ法を用いてπの値を推定します。これは、単位正方形内でランダムな点を生成し、その中に内接する単位円内の点の比率を求めることによって達成されます。以下はコードの詳細です：

1. #include <stdio.h>, <stdlib.h>, <math.h>, <time.h>: 必要なヘッダファイルをインクルードします。
2. 変数の宣言:
   • isample: モンテカルロシミュレーションの現在の繰り返しを表すループ変数。
   • nsample: 生成されるモンテカルロサンプルの数（10,000に設定）。
   • ncount: 単位円内の点の数を追跡するためのカウンタ。
   • x, y: 0から1までの間で生成されたランダムな数値を格納する変数。
   • r: 点（x, y）から原点までのユークリッド距離。
3. srand(time(NULL)): ランダム数生成器を初期化します。
4. fp = fopen("montecarlo.out", "w"): "montecarlo.out" という名前のファイルを書き込み用に開きます。このファイルにはシミュレーションの結果が保存されます。
5. for (isample = 1; isample <= nsample; isample++): 指定されたサンプル数（nsample）のループを開始します。
6. x = (double)rand() / RAND_MAX および y = (double)rand() / RAND_MAX: ランダムな数値 x および y を生成します。両方とも0から1の間です。
7. r = sqrt(x * x + y * y): 点（x, y）から原点までのユークリッド距離を計算します。
8. if (r <= 1.0) ncount++: 点（x, y）が単位円内にあるかどうかを確認します（原点からの距離が1未満）。Trueの場合、カウンタ ncount を増やします。
9. fprintf(fp, "%10d %10d %26.16e\n", isample, ncount, 4.0 * ncount / (double)isample): ファイルにフォーマットされた出力を書き込みます。現在のサンプリングに基づく、現在のシミュレーションによる π の推定値が含まれます。
10. fclose(fp): 出力ファイルを閉じます。

要約すると、このプログラムは単位正方形内でランダムな点を生成し、単位円内の点の割合に基づいて π を推定するモンテカルロシミュレーションを実施します。シミュレーションの結果は "montecarlo.out" という名前のファイルに記録されます。

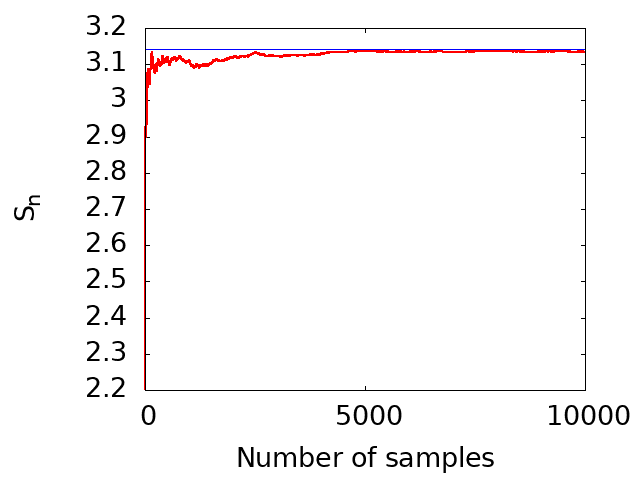
以下の図は、前述のコードを使用して推定された π の値をサンプリングポイントの数の関数として視覚的に表現しています。図から明らかなように、サンプリングポイントの数が増加するにつれて、その値は正確な π の値（おおよそ3.14）に収束し、大きなサンプリングの極限での収束を示しています。

Lesson 5-2：積分のためのモンテカルロ法

このレッスンでは、関数の積分に対するモンテカルロ法を探求します。積分を考えてみましょう： \begin{align} S = \int_a^b dx f(x). \tag{1}

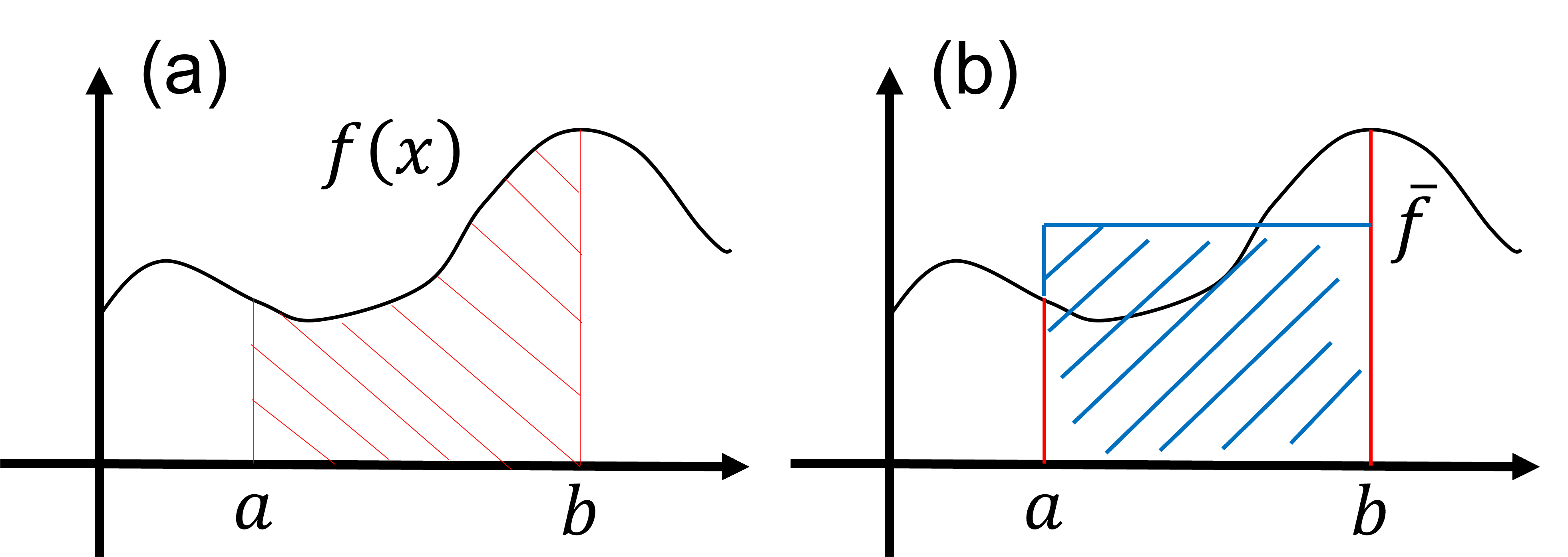
積分のためのモンテカルロ法は、平均値 \( \bar{f} \) を計算することを含みます。モンテカルロ法の積分の中核アルゴリズムでは、式 (\(1\)) を積分するために区間 \((a \le x \le b) \) 内で多くのランダムな数 \(x_i\) が生成されます。そして、平均値 \( \bar{f} \) は以下のように近似されます： \begin{align} \bar{f} \approx \frac{1}{N} \sum_{i=1}^N f(x_i), \tag{3}

モンテカルロ法に慣れるために、以下の積分を評価するC言語プログラムを開発してみましょう： \begin{align} S = \int_0^1 dx \frac{4}{1+x^2}. \tag{5}

以下のC言語コードは、モンテカルロ法を使用して式 (\(5\)) の値を推定する実装の例です。

(lesson5_2.c)

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

int main() {
    int isample, nsample;
    double x, f, s;
    FILE *file;

    nsample = 10000;

    s = 0.0;
    file = fopen("pi_montecarlo.out", "w");

    for (isample = 1; isample <= nsample; isample++) {
        x = (double)rand() / RAND_MAX;
        f = 4.0 / (1.0 + x * x);
        s = s + f;
        fprintf(file, "%10d  %26.16e\n", isample, s / isample);
    }

    fclose(file);

    return 0;
}

このC言語プログラムは、πの値を推定するためのモンテカルロシミュレーションを実行します。以下はコードの詳細です：

1. #include <stdio.h>, <stdlib.h>, <time.h>: 必要なヘッダファイルをインクルードします。
2. 関数 f(x): 関数 4.0 / (1.0 + x * x) を定義します。
3. 変数の宣言:
   • isample: モンテカルロシミュレーションの現在の繰り返しを表すループ変数。
   • nsample: 生成されるモンテカルロサンプルの数（10,000に設定）。
   • x: 0から1までの間で生成されるランダムな数値を格納する変数。
   • s: 関数値の合計を累積する変数。
4. srand(time(NULL)): ランダム数生成器を初期化します。
5. fp = fopen("pi_montecarlo.out", "w"): "pi_montecarlo.out" という名前のファイルを書き込み用に開きます。このファイルにはシミュレーションの結果が保存されます。
6. for (isample = 1; isample <= nsample; isample++): 指定されたサンプル数（nsample）のループを開始します。
7. x = (double)rand() / RAND_MAX: ランダムな数値 x を0から1まで生成します。
8. s += f(x): 生成されたランダムな数値 x に基づいて関数値を累積します。
9. fprintf(fp, "%10d %26.16e\n", isample, s / isample): ファイルにフォーマットされた出力を書き込みます。現在のサンプル番号（isample）と累積された関数値の実行平均が含まれており、これを使用してπを推定します。
10. fclose(fp): 出力ファイルを閉じます。

要約すると、このプログラムはπの値を推定するためのモンテカルロシミュレーションを実行し、ランダムな点が生成され、それらが特定の数学的な関数への寄与が累積されます。累積値の実行平均を使用してπの値を近似し、結果は "pi_montecarlo.out" という名前のファイルに書き込まれます。

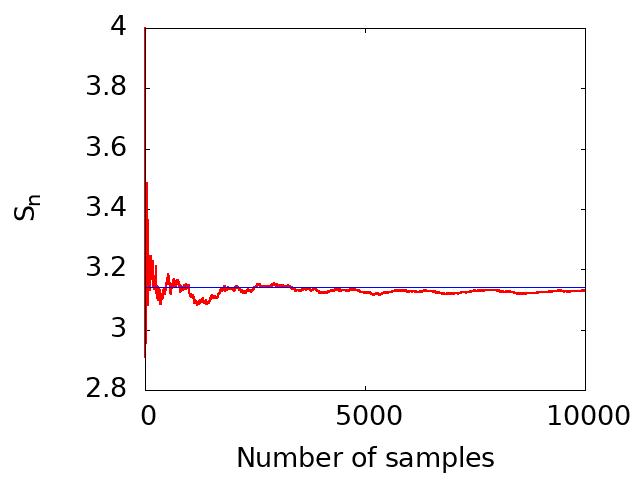
以下の図は、上記のコード (lesson5_2.c) を用いたπの推定値をサンプリングポイントの数の関数として視覚的に示しています。図から明らかなように、サンプリングポイントの数が増加するにつれて、その値は正確なπの値（おおよそ3.14）に収束しています。大きなサンプリングの極限での収束が確認できます。