Lesson 5: モンテカルロ法
Lesson 5-1：モンテカルロ法の例（円周率の計算）
この節では、モンテカルロ法について学びます。モンテカルロ法は、乱数を用いた数値計算手法です。
以下のPythonコードは、円周率 (π) の値を推定するためのモンテカルロ法の実装です。この方法は統計的確率の原理に基づいており、数値結果を得るために乱数を使用します。
import matplotlib.pyplot as plt
import random
# Number of random points to generate
n = 10000
# Initializing counters for points inside and outside the circle
num_inside_circle = 0
num_outside_circle = 0
# Lists for storing points for plotting
x_inside = []
y_inside = []
x_outside = []
y_outside = []
# Generating random points and calculating Pi
for _ in range(n):
x, y = random.random(), random.random()
distance = x**2 + y**2
if distance <= 1:
num_inside_circle += 1
x_inside.append(x)
y_inside.append(y)
else:
num_outside_circle += 1
x_outside.append(x)
y_outside.append(y)
# Estimating Pi
pi_estimate = 4 * num_inside_circle / n
# Plotting the points
plt.figure(figsize=(6,6))
plt.scatter(x_inside, y_inside, color='blue', s=1)
plt.scatter(x_outside, y_outside, color='red', s=1)
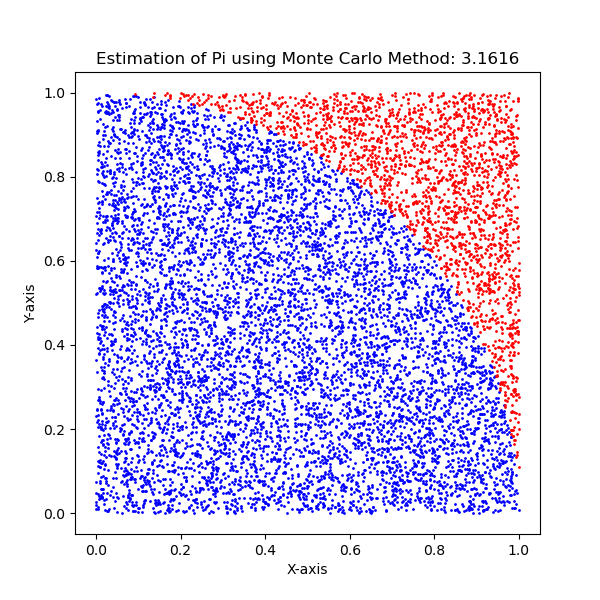
plt.title(f'Estimation of Pi using Monte Carlo Method: {pi_estimate}')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.savefig('pi_mc.png')
plt.show()以下に、このコードの解説を示します：
1. ライブラリのインポート
matplotlib.pyplot：結果を描画するために使用されます。random：乱数を生成するために使用されます。
2. 初期化
n = 10000：生成されるランダム点の数を定義します。num_inside_circleとoutside_circle：それぞれ単位円の内側と外側に打たれた点の数を数えるためのカウンター変数です。x_inside,y_inside,x_outside,y_outside：プロットのための点の座標を格納するリストです。
3. ランダム点の生成と円周率の推定
- ランダム点を生成するために
n回実行するループ。 - 各イテレーションで、点
(x, y)はxとyが0と1の間のランダムな数で生成されます。 - 原点
(0,0)から点までのdistanceは式 \( \text{distance} = x^2 + y^2 \) を使用して計算されます。 - 距離が1以下であれば、その点は単位円の内側にあり、
inside_circleカウンターが増加します。点の座標もx_insideとy_insideリストに追加されます。 - 距離が1より大きい場合、その点は単位円の外側に落ち、
outside_circleカウンターが増加します。点の座標はx_outsideとy_outsideリストに追加されます。
4. 円周率の推定
- 円周率の推定値は式 \( \pi_{\text{estimate}} = 4 \times \frac{\text{inside_circle}}{n} \) を使用して計算されます。
- この式は、円の面積と四角形の面積の比率から導き出されます。四角形の側面が1（円の半径）であるため、四角形の面積は1であり、円の面積はπ/4です。したがって、円内の点の比率と総点数はπ/4を近似します。
5. 点のプロット
- Matplotlibを使用して散布図が作成されます。
- 円内の点は青でプロットされ、円外の点は赤でプロットされます。
- プロットは円周率の推定値でタイトルされ、X軸とY軸でラベル付けされます。
6. 円周率の推定値の表示
- 最後に、円周率の推定値が表示されます。
この方法は確率論的なアプローチであり、生成されるランダム点の数が増えることで推定の精度が向上します。このプロットは、ランダムサンプリングが単位正方形と単位円の面積をどのようにカバーするかを視覚的に示し、モンテカルロ推定の背後にある概念を説明しています。
上記のPythonコードは、ランダムに点を生成し、それらが単位円の内側か外側かをチェックすることによって、モンテカルロ法を使用して円周率の値を推定します。このシミュレーションでは、10,000点が生成されました。
以下の図は、これらの点の分布を視覚的に表しており、円内の点は青色、円外の点は赤色で示されています。このアプローチは、円の面積と四角形の面積の比率を利用して円周率の値を近似します。この推定の精度は、シミュレーションに使用される点の数が増えることで向上します。
Lesson 5-2：積分のためのモンテカルロ法
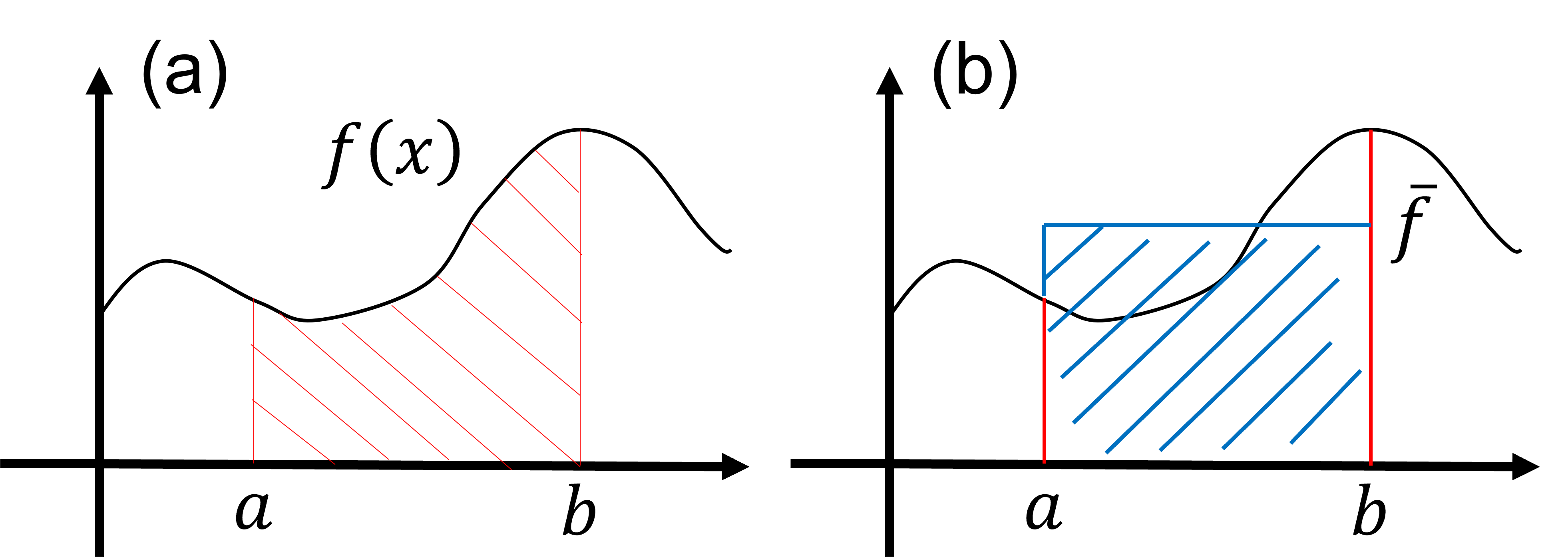
ここでは、モンテカルロ法を使用して関数を積分する方法を学びます。以下の積分を考えてみましょう： \begin{align} S=\int^b_a dx f(x). \tag{1} \end{align} 積分の値 \(S\) は、下の図 (a) で赤色に塗られた領域に対応します。積分の値は、図 (b) で青色に塗られた領域にも相当することに注意することが重要です。これは \begin{align} S=\int^b_a dx f(x)= (b-a)\times \bar f, \tag{2} \end{align} によって記述されます。ここで \(\bar f \) は関数 \(f(x)\) の範囲 \((a\le x \le b)\) での平均値です。この観察から、積分の値 \(S\) は、積分の範囲における関数 \( f(x) \) の平均値 \(\bar f \) を使用して評価できることが示唆されます。
積分のためのモンテカルロ法は、平均値 \( \bar f \) の評価に基づいています。積分の式(\(1\))の評価のためのモンテカルロ法の最も基本的なアルゴリズムでは、範囲 \((a \le x \le b) \) 内で多くのランダム数 \(x_i\) が生成されます。次に、平均値 \( \bar f \) は以下のように近似されます： \begin{align} \bar f \approx \frac{1}{N} \sum^N_{i=1}f(x_i), \tag{3} \end{align} ここで \(N\) は生成されたランダム数の数です。したがって、式 \((1)\) の積分は以下のように近似されます： \begin{align} S=\int^b_a dx f(x)= (b-a)\times \bar f \approx \frac{b-a}{N}\sum^N_{i=1}f(x_i) \tag{4} \end{align} 範囲 \((a\le x \le b)\) 内で生成されたランダム数 \(\{x_i \}\) を用いて。
モンテカルロ法に慣れるために、以下の積分を評価するPythonプログラムを書いてみましょう： \begin{align} S=\int^1_0 dx \frac{4}{1+x^2}. \tag{5} \end{align} 式 \( (5)\) を解析的に積分することで \(S=\pi\) を得ることができます。
以下のPythonコードは、式 \((5)\) の \(S\) の値を推定するためのモンテカルロ法の実装です。
import random
# Number of random points to use for the Monte Carlo simulation
n = 10000
# Function to integrate
def f(x):
return 4.0/(1.0 + x**2)
# Monte Carlo integration
integral = 0.0
for _ in range(n):
integral = integral + f(random.random())
integral = integral / n
print('integral =',integral)上記のPythonコードは、数値積分にモンテカルロ法を使用する例です。以下にその構成要素と機能の詳細な分解を示します：
- ランダムモジュールのインポート：コードはランダムな数を生成するために使用される
randomモジュールをインポートしています。 - ランダムポイントの数（n）の設定：変数
nは10,000に設定され、シミュレーションで使用されるランダムポイントの数を表しています。一般に、数が多いほど近似値は正確になります。 - 積分する関数（f(x)）：関数
f(x)は4.0 / (1.0 + x**2)として定義されています。この関数はπの数値を計算するために使用される式の一部です。 - モンテカルロ積分：
- 変数
integralは0.0に初期化され、関数値の合計を蓄積します。 - forループが
n回実行され、その都度：random.random()を使用して0から1の間のランダム数を生成します。- このランダム数での
f(x)の結果をintegralに加えます。
- ループの後、
integralにはすべてのランダムポイントのf(x)の合計が保持されます。
- 変数
- 近似積分の計算：
integralの合計はnで割られ、[0, 1]の範囲での積分を近似する平均値を得るために使用されます。 - 結果の印刷：計算された近似積分が印刷されます。
要約すると、このコードは特定の区間で関数の積分を推定するためのモンテカルロ法の実装です。この場合、[0, 1]の範囲での4/(1 + x^2)の積分を近似することで、πの値を推定する方法です。この近似の正確さは使用されるランダムポイントの数に依存します。
Lesson 5-3: 一般分布を用いたモンテカルロ法
前のセクションでは、一様分布からのランダム数を使用したモンテカルロ法について学びました。このセクションでは、一様分布の代わりに一般分布を使用してモンテカルロ法を適用する方法を探ります。次の積分を考えてください： \[ S = \int^{\infty}_{-\infty}dx f(x) w(x), \tag{6} \] ここで \( w(x) \) はどこでも非負の分布関数（つまり、任意の \( x \) に対して \( w(x) \ge 0 \)）であり、正規化されています（\( \int^{\infty}_{-\infty} dx w(x) = 1 \)）。分布関数 \( w(x) \) が非負性と正規化の条件を満たす限り、式 (6) の積分は、以下の合計で示されるように、\( w(x) \) に従って分布されたランダム数を使用して評価することができます： \[ S = \int^{\infty}_{-\infty}dx f(x) w(x) \approx \frac{1}{N}\sum^{N}_{i=1} f(x_i), \tag{7} \] ここで \( N \) はランダム数の数であり、\( \{x_i\} \) は確率分布関数 \( w(x) \) に従って生成されたランダム数です。
Pythonのrandomモジュールは、一様分布、指数分布、正規分布など、さまざまな分布のランダム数を生成するためのサポートを提供しています。さらに、メトロポリスサンプリングを使用することで、任意の分布からランダム数を生成することもできます。
ここでは、モンテカルロ法で一般分布を使用する例を提供します。我々は、正規分布を用いる次の積分の計算を考えます：
\[ S=\int^{\infty}_{-\infty}dx x^2 \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}=1. \tag{7} \]
以下のPythonコードは、式 (7) の \( S \) の値を推定するためのモンテカルロ法の実装です。（Pythonコードはここにあります）
import numpy as np
# Number of random points to use for the Monte Carlo simulation
n = 10000
# Function to integrate
def f(x):
return x**2
# Monte Carlo integration
integral = 0.0
for _ in range(n):
integral = integral + f(np.random.normal(0, 1))
integral = integral / n
print('integral =',integral)Lesson 5-4：重要度サンプリング
このセクションでは、積分関数に対応する適切な分布関数を使用することでモンテカルロサンプリングの収束を改善する技術について学びます。積分を次のように変更することを考えます：
\begin{align} S=\int^{\infty}_{-\infty}dx f(x) =\int^{\infty}_{-\infty}dx \frac{f(x)}{w(x)}w(x), \tag{8} \end{align}
ここで、\( w(x) \) は正規化条件 \(\int^{\infty}_{-\infty}dx w(x)= 1\) を満たし、正の値を保証する \( w(x) > 0 \) の分布関数です。レッスン5-3からの概念を活用して、式 (8) の積分をモンテカルロサンプリングを使用して評価することができます。これは、分布関数 \( w(x) \) に従ってランダム数をサンプリングすることで行われ、以下の近似で示されます：
\begin{align} S = \int^{\infty}_{-\infty}dx \frac{f(x)}{w(x)}w(x) \approx \frac{1}{N}\sum^N_i \frac{f(x_i)}{w(x_i)}, \tag{9} \end{align} ここで、\( N \) は使用されるランダム数の数を表し、\( \{x_i\} \) は \( w(x) \) からサンプリングされたランダム数です。
式 (9) で示されるモンテカルロサンプリングの収束速度は、比率 \(\frac{f(x_i)}{w(x_i)}\) の変動に影響されます。この比率が \(x\) に依存しない定数であるシナリオを考えてみます。そのような場合、単一のモンテカルロサンプルでも収束結果を得ることができます。典型的なシナリオでより速い収束を達成するためには、\(f(x)\) によく似た分布関数 \(w(x)\) を選択することが有益です。この類似性はサンプリングされた値 \(\frac{f(x_i)}{w(x_i)}\) の変動を最小限に抑え、より早い収束につながります。本質的に、積分関数 \(f(x)\) が大きい領域で分布関数 \(w(x)\) が増加すると、モンテカルロサンプリングはより迅速に収束します。サンプリング効率を改善するために最適な分布関数を選択するこのアプローチは重要度サンプリングとして知られています。