<前のページへ: 1階常微分方程式 |次のページへ: モンテカルロ法>

Lesson 4: 2階常微分方程式の数値解法

このページでは、C言語を用いて2階常微分方程式を数値的に解く方法について学びます。

他のプログラミング言語を利用する方は以下のページも参考にしてください:
Pythonで2階常微分方程式を解く
Juliaで2階常微分方程式を解く
Fortranで2階常微分方程式を解く

---

次の形で書くことができる2階常微分方程式を数値的に解く方法を学びます: \[ \frac{d^2y(x)}{dx^2}=f\left (x,y(x), \frac{dy(x)}{dx} \right). \tag{1} \] このような二階常微分方程式には、ニュートンの運動方程式 \(m\frac{d^2x(t)}{dt^2}=F(t)\) が含まれます。

2階常微分方程式を解くための方法にはいくつかの種類があります。ここでは、補助変数 \(s(x)=\frac{dy(x)}{dx}\) を導入し、次のような2変数の連立1階常微分方程式に書き換えます： \[ \frac{ds(x)}{dx} =f\left (x,y(x), s(x)\right), \tag{2} \] \[ \frac{dy(x)}{dx} =s(x). \tag{3} \]

オイラー法による解法

以下のC言語のソースコードは、オイラー法を使用して連立一階微分方程式を解く方法を示しています。

(lesson4_1.c)

#include <stdio.h>
#include <math.h>

int main() {
    double k, m;
    double x, v, f;
    double x_new, v_new;
    double x_exact, v_exact;
    double t_fin, dt, t;
    int n, i;
    FILE *file;

    n = 20;
    t_fin = 10.0;
    dt = t_fin / n;

    k = 1.0;
    m = 1.0;

    x = 0.0;
    v = 1.0;

    file = fopen("newton_euler.out", "w");

    t = 0.0;
    x_exact = sin(t);
    v_exact = cos(t);

    fprintf(file, "%16.6e%16.6e%16.6e%16.6e%16.6e\n", t, x, v, x_exact, v_exact);

    for (i = 0; i < n; i++) {
        f = -k * x;
        x_new = x + dt * v;
        v_new = v + dt * f / m;

        t = dt * (i + 1);
        x_exact = sin(t);
        v_exact = cos(t);

        fprintf(file, "%16.6e%16.6e%16.6e%16.6e%16.6e\n", t, x_new, v_new, x_exact, v_exact);

        x = x_new;
        v = v_new;
    }

    fclose(file);

    return 0;
}

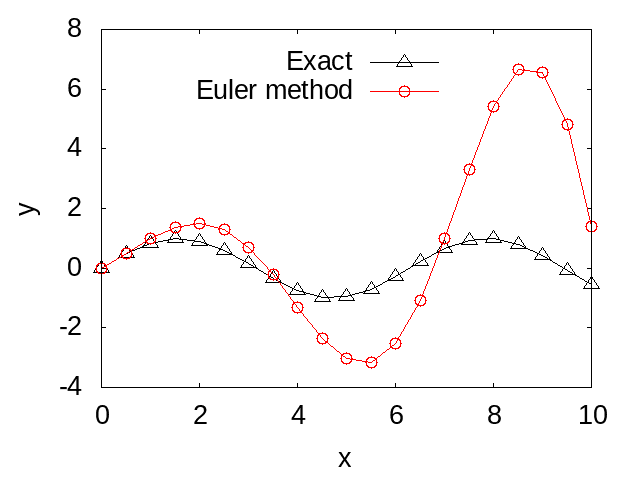
このプログラムを実行すると、オイラー法による数値解と解析解の比較が得られます。下図はその結果を示しています。

予測子・修正子法

次に、予測子・修正子法を用いて2階常微分方程式を解く方法について学びます。

(lesson4_2.c)

#include <stdio.h>
#include <math.h>

int main() {
    double k, m;
    double x, v, f;
    double x_pred, v_pred, f_pred;
    double x_new, v_new;
    double x_exact, v_exact;
    double t_fin, dt, t;
    int n, i;
    FILE *file;

    n = 20;
    t_fin = 10.0;
    dt = t_fin / n;

    k = 1.0;
    m = 1.0;

    x = 0.0;
    v = 1.0;

    file = fopen("newton_PredCorr.out", "w");

    t = 0.0;
    x_exact = sin(t);
    v_exact = cos(t);

    fprintf(file, "%16.6e%16.6e%16.6e%16.6e%16.6e\n", t, x, v, x_exact, v_exact);

    for (i = 0; i < n; i++) {
        f = -k * x;
        x_pred = x + dt * v;
        v_pred = v + dt * f / m;
        f_pred = -k * x_pred;

        x_new = x + dt * 0.5 * (v + v_pred);
        v_new = v + dt * 0.5 * (f + f_pred) / m;

        t = dt * (i + 1);
        x_exact = sin(t);
        v_exact = cos(t);

        fprintf(file, "%16.6e%16.6e%16.6e%16.6e%16.6e\n", t, x_new, v_new, x_exact, v_exact);

        x = x_new;
        v = v_new;
    }

    fclose(file);

    return 0;
}

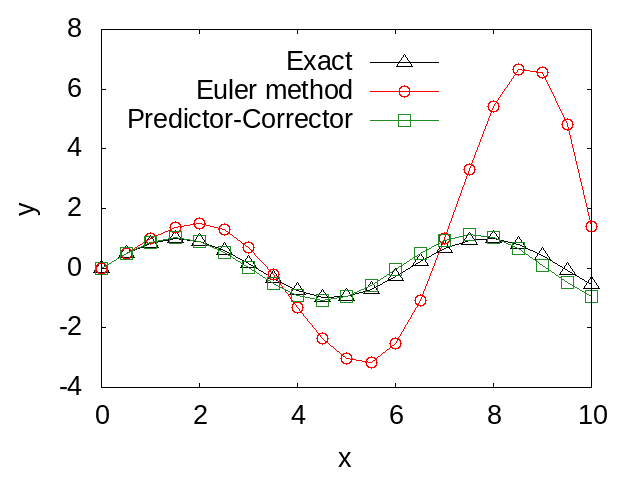
以下の図は、得られた数値解と解析解の比較を示しています。予測子・修正子法は、オイラー法よりも精度が高いことがわかります。

---

<前のページへ: 1階常微分方程式 |次のページへ: モンテカルロ法>

[Cホームへ戻る]

---