<前のページ: 1階常微分方程式の数値解法|次のページ: モンテカルロ法>
Lesson 4: 2階常微分方程式の数値解法
このページでは、Fortranを用いて2階常微分方程式を数値的に解く方法について学びます。
Fortran以外のプログラミング言語を利用の方は以下のページも参考にしてみてください:
Pytohnで1階常微分方程式を解く
Juliaで1階常微分方程式を解く
二階常微分方程式は一般に次のような形に書くことが出来ます。 \[ \frac{d^2y(x)}{dx^2} =f\left (x,y(x), \frac{dy(x)}{dx} \right). \tag{1} \] ここでは、二階常微分方程式を解くために、式(1)を次のような一階の連立微分方程式に書き換えることを考えます。 \[ v(x) = \frac{dy(x)}{dx}, \tag{2} \] \[ \frac{dv(x)}{dx} = f\left (x,y(x), v(x) \right). \tag{3} \] ここで、新たに変数\(v(x)=dy(x)/dx\)を導入することで、二階微分方程式を二つの連立微分方程式に書き換えています。このような一階の連立微分方程式は、前ページの(1階常微分方程式の解法)で学んだ方法を用いて数値的に解くことが出来ます。また、一般に、n階の微分方程式は\(n\)個の一階常微分方程式から成る連立微分方程式に書き換えることが出来ます。
Lesson 4-1: オイラー法
ここではまず、オイラー法を用いて二階常微分方程式を解く方法について学ぶ。オイラー法の詳細は前ページ(1階常微分方程式の解法)で説明しているので、詳細はそちらを参照してください。
オイラー法を用いた2階常微分方程式の解法について学ぶために、ここでは調和振動子に対するNewton方程式を例にして微分方程式を解いていきます。調和振動子に対するNewtonの運動方程式は次のように書けます。 \[ m \frac{d^2x(t)}{dt^2}=-k x(t). \tag{4} \] ここで\(m\)は粒子の質量であり、\(k\)はばね定数です。上で議論されたように、この二階上微分方程式を次のような二つの一階連立常微分方程式に書き換えることを考えます: \[ v(t)=\frac{dx(t)}{dt}, \tag{5} \] \[ \frac{dv(t)}{dt} = -\frac{k}{m}x(t). \tag{6} \] ここで、\(v(t)\)は粒子の速度を表します。これらの連立微分方程式,式(5)と式(6),を次の初期条件の下で解くことを考えてみましょう。 \[ x(0)=0, \tag{7} \] \[ v(0)=1. \tag{8} \] この連立微分方程式の解は解析的に求めることができ、次のように与えられます。 \[ x(t)=\sqrt{\frac{m}{k}} \sin \left [ \sqrt{\frac{k}{m}}t \right ], \tag{9} \] \[ v(t)=\cos \left [\sqrt{\frac{k}{m}}t \right ]. \tag{10} \]
以下のプログラム例では上記の微分方程式(Newton方程式)をオイラー法を用いて解いています。
program main
implicit none
real(8) :: k, m
real(8) :: x, v, f
real(8) :: x_new, v_new
real(8) :: x_exact, v_exact
real(8) :: t_fin, dt, t
integer :: n, i
n = 20
t_fin = 10d0
dt = t_fin/n
k = 1d0
m = 1d0
x = 0d0
v = 1d0
open(20,file="newton_euler.out")
t = 0d0
x_exact = sin(t)
v_exact = cos(t)
write(20,"(5e16.6e3)")t,x,v,x_exact,v_exact
do i = 0, n-1
f = -k*x
x_new = x + dt*v
v_new = v + dt*f/m
t = dt*(i+1)
x_exact = sin(t)
v_exact = cos(t)
write(20,"(5e16.6e3)")t,x_new,v_new,x_exact,v_exact
x = x_new
v = v_new
end do
close(20)
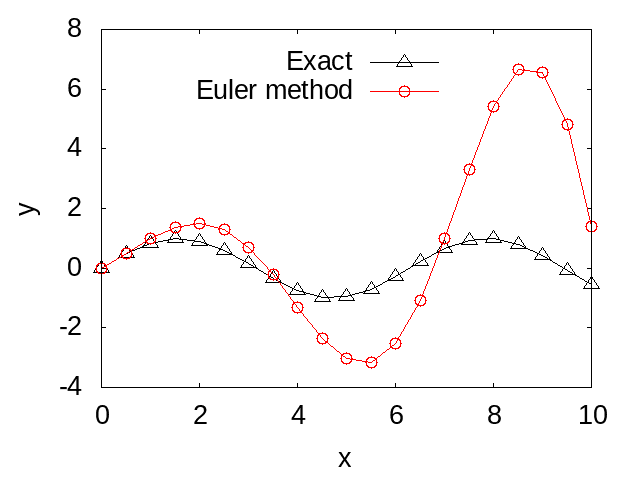
end program main以下の図では、上記のプログラムによって計算したオイラー法による数値解と解析解を比較しています。時間の経過とともに、数値解と解析解の差が大きくなっていく様子が確認できます。この誤差は、オイラー法が差分近似に基づいていることによるもので、時間の刻み幅を小さくすることで改善することが出来ます。しかしながら、刻み幅を小さくすることによるオイラー法の制度の改善は非常に遅いため、実用的な計算に用いられることは多くはありません。次の節では、オイラー法のアルゴリズムを改善した予測子・修正子法によって二階上微分方程式(Newton方程式を含む)を解く方法について学びます。
Lesson 4-2: 予測子・修正子法
ここでは、予測子・修正子法によってNewton方程式,式(1)を解くことを試みます。予測子・修正子法の詳細については「1階常微分方程式の数値解法」を参照してください。
以下のプログラム例では予測子・修正子法によって上記のNewton方程式を解いています。
program main
implicit none
real(8) :: k, m
real(8) :: x, v, f
real(8) :: x_pred, v_pred, f_pred
real(8) :: x_new, v_new
real(8) :: x_exact, v_exact
real(8) :: t_fin, dt, t
integer :: n, i
n = 20
t_fin = 10d0
dt = t_fin/n
k = 1d0
m = 1d0
x = 0d0
v = 1d0
open(20,file="newton_PredCorr.out")
t = 0d0
x_exact = sin(t)
v_exact = cos(t)
write(20,"(5e16.6e3)")t,x,v,x_exact,v_exact
do i = 0, n-1
f = -k*x
x_pred = x + dt*v
v_pred = v + dt*f/m
f_pred = -k*x_pred
x_new = x + dt*0.5d0*(v+v_pred)
v_new = v + dt*0.5d0*(f+f_pred)/m
t = dt*(i+1)
x_exact = sin(t)
v_exact = cos(t)
write(20,"(5e16.6e3)")t,x_new,v_new,x_exact,v_exact
x = x_new
v = v_new
end do
close(20)
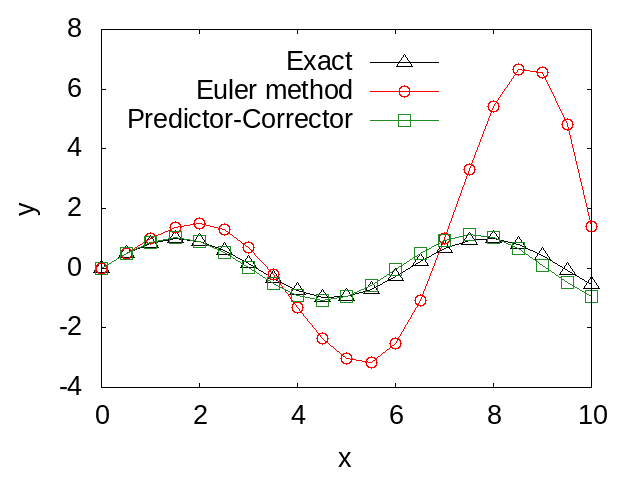
end program main下図では、上記のプログラムを利用して得られた予測子・修正子法による数値解をオイラー法による数値解、及び解析解と比較しています。図から、予測子・修正子法の精度がオイラー法の精度より改善されていることが確認できます。また、予測子・修正子法も差分近似に基づいているため、時間刻み幅を小さくすることによって誤差を小さくすることができます。
Lesson 4-3: Runge-Kutta法
ここでは、Runge-Kutta法を用いてNewton方程式,式(\(1\)),を解くプログラムを実装します。Runge-Kutta法の詳細については前回の議論(Lesson 3)を参照してください。
以下のプログラム例では、Runge-Kutta法を用いてNewton方程式を解いています。
program main
implicit none
real(8) :: k, m
real(8) :: x, v, f
real(8) :: kx1,kx2,kx3,kx4
real(8) :: kv1,kv2,kv3,kv4
real(8) :: x_new, v_new
real(8) :: x_tmp, v_tmp
real(8) :: x_exact, v_exact
real(8) :: t_fin, dt, t
integer :: n, i
n = 20
t_fin = 10d0
dt = t_fin/n
k = 1d0
m = 1d0
x = 0d0
v = 1d0
open(20,file="newton_RungeKutta.out")
t = 0d0
x_exact = sin(t)
v_exact = cos(t)
write(20,"(5e16.6e3)")t,x,v,x_exact,v_exact
do i = 0, n-1
f = -k*x
kx1 = v
kv1 = f/m
x_tmp = x + 0.5d0*dt*kx1
v_tmp = v + 0.5d0*dt*kv1
kx2 = v_tmp
f = -k*x_tmp
kv2 = f/m
x_tmp = x + 0.5d0*dt*kx2
v_tmp = v + 0.5d0*dt*kv2
kx3 = v_tmp
f = -k*x_tmp
kv3 = f/m
x_tmp = x + dt*kx3
v_tmp = v + dt*kv3
kx4 = v_tmp
f = -k*x_tmp
kv4 = f/m
x_new = x + (dt/6d0)*(kx1+2d0*kx2+2d0*kx3+kx4)
v_new = v + (dt/6d0)*(kv1+2d0*kv2+2d0*kv3+kv4)
t = dt*(i+1)
x_exact = sin(t)
v_exact = cos(t)
write(20,"(5e16.6e3)")t,x_new,v_new,x_exact,v_exact
x = x_new
v = v_new
end do
close(20)
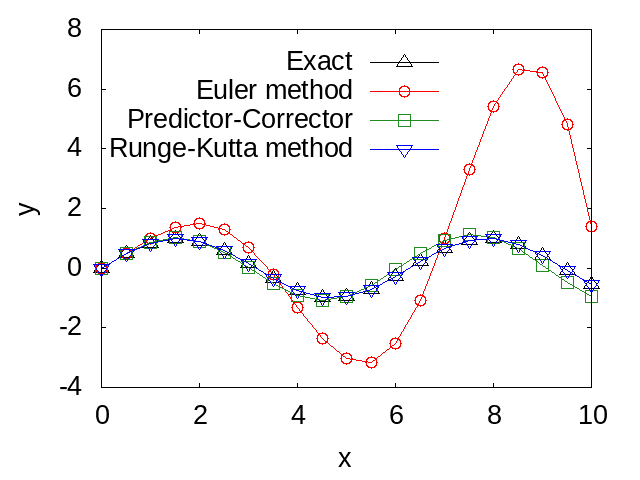
end program main以下の図では、上記のプログラムを用いて計算したRunge-Kutta法による数値解をオイラー法と予測子・修正子法による数値解、及び解析解と比較しています。図から、Runge-Kutta法によって予測子・修正子法やオイラー法より高精度な計算が実行できていることが分かります。
<前のページ: 1階常微分方程式の数値解法|次のページ: モンテカルロ法>