<前のページ: 1階の常微分方程式の求解|次のページ: モンテカルロ法>
Lesson 4: 2階の常微分方程式の求解
このページでは、Pythonを用いて2階常微分方程式を数値的に解く方法について学びます。
Python以外のプログラミング言語を利用の方は以下のページも参考にしてみてください:
C言語で2階常微分方程式を解く
Juliaで2階常微分方程式を解く
Fortranで2階常微分方程式を解く
この節では、次の形で書くことができる2階常微分方程式を数値的に解く方法を学びます。2階常微分方程式は一般に次のような形で書くことが出来ます。 \begin{align} \frac{d^2y(x)}{dx^2}=f\left (x,y(x), \frac{dy(x)}{dx} \right). \tag{1} \end{align} このような二階常微分方程式には、ニュートンの運動方程式 \(m\frac{d^2x(t)}{dt^2}=F(t)\) が含まれます。
2階常微分方程式を解くための方法にはいくつかの種類があります。ここでは、2階常微分方程式を解くために、補助変数 \(s(x)=\frac{dy(x)}{dx}\) を導入し、方程式(1)を次のような2変数の連立1階常微分方程式に書き換えます: \[ \frac{ds(x)}{dx} =f\left (x,y(x), s(x)\right), \tag{2} \] \[ \frac{dy(x)}{dx} =s(x). \tag{3} \] これは、2階微分方程式を2つの1階常微分方程式の組に書き換えることができることを示しています。このような変換により導入された1階微分方程式は、前節で学んだ1階微分方程式の数値解法を用いて解くことが出来ます。このように、2階微分方程式は、連立した1回微分方程式に変換し、1階微分方程式を解く方法を用いて求解することが出来ます。
このページでは、具体例として次の2階常微分方程式を実際に解くPythonコードを書くことで、2階常微分方程式の数値解法について学んでいきます。 \begin{align} \frac{d^2x(t)}{dt}=-x(t). \tag{4} \end{align} ここで、初期条件は\(x(0)=0, \dot x(t)=1\)です。
補助変数\(v(t)=\frac{dx(t)}{dt}\)を導入することで、方程式(4)は次の連立微分方程式として書き換えられます: \[ \frac{dx(t)}{dt} =v(t), \tag{5} \] \[ \frac{dv(t)}{dt} =-x(t). \tag{6} \] さらに、初期条件\(x(0)=0, \dot x(0)=1\)は\(x(0)=0, v(0)=1\)として書き換えることが出来ます。
Lesson 4-1: オイラー法
以下のソースコードは、オイラー法を使用して、連立一階微分方程式、方程式(5)および(6)を解くためのPythonコードです。このソースコードを参考にして、連立微分方程式を解くための自分自身のコードを作成しましょう。
from matplotlib import pyplot as plt
import numpy as np
def dxdt(v):
return v
def dvdt(x):
return -x
def euler_method(x,v,dt):
x_new = x + dt*dxdt(v)
v_new = v + dt*dvdt(x)
return x_new, v_new
tini = 0.0
tfin = 10.0
n = 24
dt = (tfin - tini)/n
time = np.linspace(tini,tfin,n+1)
xt = np.zeros(n+1)
vt = np.zeros(n+1)
# Initial conditions
xt[0] = 0.0
vt[0] = 1.0
for i in range(n):
xt[i+1], vt[i+1] = euler_method(xt[i],vt[i],dt)
# Plot the results
plt.plot(time, xt, label='x(t)')
plt.plot(time, vt, label='v(t)')
plt.plot(time, np.sin(time), label='x(t): Exact', linestyle='dashed')
plt.plot(time, np.cos(time), label='v(t): Exact', linestyle='dashed')
plt.xlabel('t')
plt.ylabel('x,v')
plt.legend()
plt.savefig("diff_2nd_Euler.png")
plt.show()下の図は、上記のソースコードを実行して得られた数値解と正確な解との比較を示しています。オイラー法によって得られた数値解は、時間\(t\)が経過するにつれて正確な解から大きく逸脱しています。
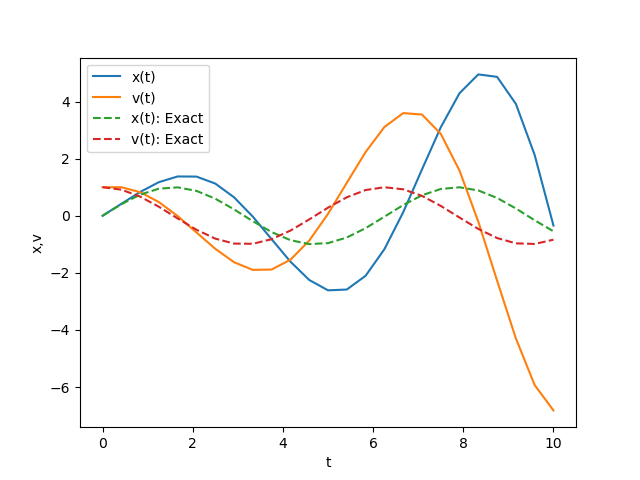
前節で学んだように、予測子-修正子法やルンゲ=クッタ法を使用して、数値解の精度を向上させることができます。以下のサンプルソースコードは、予測子-修正子法によって一連の微分方程式、方程式(5)および(6)を解くコードの例を示しています。
from matplotlib import pyplot as plt
import numpy as np
def dxdt(v):
return v
def dvdt(x):
return -x
def pred_corr_method(x,v,dt):
# prediction
x_pred = x + dt*dxdt(v)
v_pred = v + dt*dvdt(x)
# correction
x_new = x + 0.5*dt*(dxdt(v)+dxdt(v_pred))
v_new = v + 0.5*dt*(dvdt(x)+dvdt(x_pred))
return x_new, v_new
tini = 0.0
tfin = 10.0
n = 24
dt = (tfin - tini)/n
time = np.linspace(tini,tfin,n+1)
xt = np.zeros(n+1)
vt = np.zeros(n+1)
# Initial conditions
xt[0] = 0.0
vt[0] = 1.0
for i in range(n):
xt[i+1], vt[i+1] = pred_corr_method(xt[i],vt[i],dt)
# Plot the results
plt.plot(time, xt, label='x(t)')
plt.plot(time, vt, label='v(t)')
plt.plot(time, np.sin(time), label='x(t): Exact', linestyle='dashed')
plt.plot(time, np.cos(time), label='v(t): Exact', linestyle='dashed')
plt.xlabel('t')
plt.ylabel('x,v')
plt.legend()
plt.savefig("diff_2nd_PredCorr.png")
plt.show()下の図は、得られた数値解と正確な解との比較を示しています。予測子-修正子法は、オイラー法と比べて精度を大幅に向上させることができます。
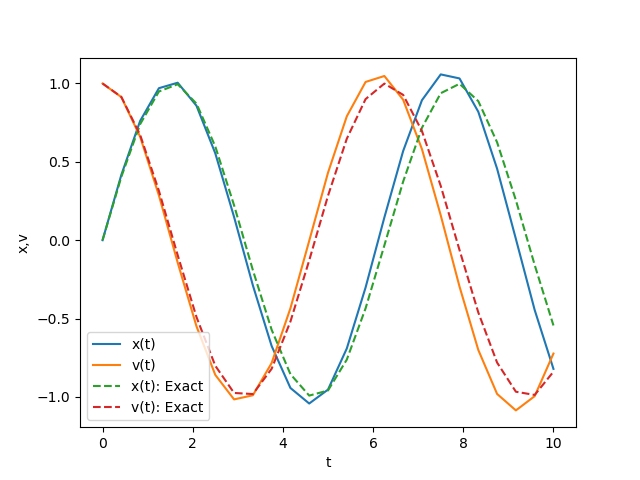
<前のページ: 1階の常微分方程式の求解|次のページ: モンテカルロ法>