Lesson 1: 数値微分

Lesson 1-1: 数値微分の基礎: 差分法を用いた近似

数値的に関数の微分を評価する前に、数学的な微分の定義を復習してみましょう。関数\(f(x)\)の微分は次の式によって定義されています: \[f'(x)=\lim_{h\rightarrow 0} \frac{f(x+h)-f(x)}{h}\] この式に基づき、十分小さな\(h\)を用いることで関数の微分\(f'(x) \)を次のように近似することが出来ます: \[f'(x) \approx \frac{f(x+h) - f(x)}{h}. \tag{1} \] このような有限の大きさの(ただし十分小さい)幅\(h\)を使って微分を近似する方法は有限差分法と呼ばれます。有限差分法による近似の誤差は、Taylor展開を用いることで次のように評価することが出来ます。例えば、関数\(f(x\))のTaylor展開は次のようになります。 \[f(x+h) = f(x) + f'(x)h +O(h^2). \tag{2}\] ここで、\(O(h^2)\)は、\(h\)の２次以上の項からなり、Taylor展開を有限の次数で打ち切った場合の誤差を表しています。式(\(2\))を変形することで次のような式を得ます。 \[f'(x) = \frac{f(x+h)-f(x)}{h}+O(h). \] したがって、有限差分近似公式, 式(\(1\)), の誤差は\(h\)に比例する事が分かります。これを\(O(h)\)[読み:オーターh]の誤差と呼びます。このことから、十分小さな\(h\)を用いることで関数の微分値\(f'(x)\)を正確に近似できることが分かります。

Talyor展開を用いることで、さらに高精度な近似公式を作ることも可能です。ここでは、関数\(f(x+h)\)と\(f(x-h)\)の2次までのTaylor展開を次のように考えてみます: \[f(x+h) = f(x) + f'(x)h + \frac{1}{2}f''(x)h^2 + O(h^3), \tag{3}\] \[f(x-h) = f(x) - f'(x)h + \frac{1}{2}f''(x)h^2 + O(h^3). \tag{4}\] ここで式(\(3\))と式(\(4\))の差を取ることによって次のような近似公式を導くことが出来ます: \[f'(x) = \frac{f(x+h)-f(x-h)}{2h} +O(h^2). \tag{5}\] この有限差分近似公式,式(\(5\)),の誤差は\(h^2\)に比例しており、\(h\)が小さい極限で式(\(2\))の差分公式よりも速く厳密な微分値に収束することが分かります。このことから、十分小さな\(h\)に対して、式(\(5\))の方が式(\(2\))よりも高精度な近似公式となっていることが分かります。式(\(2\))のような差分公式は前進差分公式と呼ばれ、式(\(5\))のような差分公式は中心差分公式と呼ばれています。

Fortranを使った数値微分の計算コード

この節では、前進差分公式と中心差分公式を用いた数値微分のFortranコードの書き方について学びます。具体的な例題として、指数関数,\(f(x)=e^x\) at \( x=0 \),の\( x=0 \)における微分を考えます。次のコードでは、関数の微分値, \( f'(0) \),を差分幅, \(h\),を変えながら計算し、厳密な微分値からの誤差を評価します。数値微分の誤差を厳密な微分値からのずれとして定義しています: \( Error = \left|f'_{numerical}(0)-f'_{exact}(0) \right| \).

(lesson1_1.f90)

program main
  implicit none
  integer :: i, n
  real(8) :: ff_0, ff_p, ff_m, dfdx_f, dfdx_m, dfdx_e
  real(8) :: x, h

  x = 0d0
  dfdx_e = exp(x)
  
  h = 1d0
  
  n = 16
  open(20,file="fd_error.out")
  do i = 1, n
     ff_0   = exp(x)
     ff_p = exp(x+h)
     ff_m = exp(x-h)

     dfdx_f = (ff_p-ff_0)/h
     dfdx_m = (ff_p-ff_m)/(2d0*h)

     write(20,"(5e16.6e3)")h,dfdx_f,abs(dfdx_f - dfdx_e),dfdx_m,abs(dfdx_m - dfdx_e)
     
     h = h/2d0
  end do
  close(20)

  
end program main

上のコードでは、\(x=0\)における微分の値を計算しています。このため、コードの7行目で変数xにはx=0を代入しています。また、8行目では、関数の厳密な微分値をdfdx_e = exp(x)によって計算しています。

コードの13行目で計算結果をファイルに出力するために、open文を使ってファイルを開いています。ここでは次の文を使ってファイルを開いています:

open(20,file="fd_error.out")

ここで番号20は装置番号を表し、ファイル名がこの整数値(装置番号)に割り当てられます。装置番号は、任意の自然数を割り当てることが出来、ファイル名の代わりにそのファイルを指し示す番号として用いられます。ここではfd_error.outという名前のファイル開くためにfile="fd_error.out"と記述されています。したがって、このようなopen文により、ここではfd_error.outという名前のファイルが開かれ、装置番号20に割り当てられます。

上記のコードでは14行目よりdoループが始まります。doループの中では、刻み幅\(h\)を変えながら繰り返し数値微分の評価が行われています。初めに、間数値, \( \exp(x) \), \( \exp(x+h) \), \( \exp(x-h) \),を評価し、それぞれを変数ff_0, ff_p, ff_m,に代入します。次に、前進差分公式, Eq. (\(1\)),の評価値を変数dfdx_f.に代入しています。同様に、中心差分公式, Eq. (\(5\)),による評価値を変数dfdx_mに代入しています。

コードの22行目では、計算結果を次のwrite文によってファイルに出力しています:

write(20,"(5e16.6e3)")h,dfdx_f,abs(dfdx_f - dfdx_e),dfdx_m,abs(dfdx_m - dfdx_e)

ここでは、装置番号20に割り当てられたファイルfd_error.outに、write文によって計算結果を出力しています。このwrite文では、結果の出力形式を"5e16.6e3"によって定義しています。ここで、最初の数値5は5つの変数の出力を表しています。その次のeは指数形式での出力フォーマットをしています。次の16.6では出力の際に16文字分のスペースを確保し、6桁分の仮数部を表示する形式で出力されること意味します。実際の出力結果を見ることで、この出力の意味を確認することが出来ます。

このdoループの最後で刻み幅hを半分にし、doループの先頭に戻って上記の処理を繰り返します。

既定の回数の反復を終えるとDOループを抜けて、26行のclose文でファイルを閉じてプログラムを終了します。

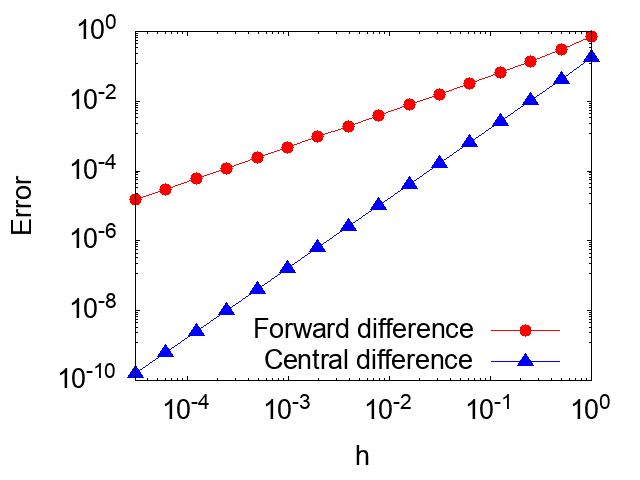
下の図では、上記のプログラムによって出力されたfd_error.outの結果を図示して、数値微分の誤差を刻み幅\(h\)の関数として示したものです。図から分かるように、中心差分公式(Central difference)による微分の評価の誤差は、前進差分公式(Forward difference)による誤差に比べて、刻み幅\(h\)が小さくなると共に急激に小さくなっています。したがって、上で議論されたように、\(h\)が小さくなる極限で、中心差分公式の誤差が前進差分による誤差よりも速くゼロに収束することが確認できます。

Lesson 1-2: 2階微分の数値的取り扱い

上記のLesson 1-1で取り上げた1階微分を数値的に評価する数値微分の拡張として、2階の微分を数値的に取り扱う方法について学びます。式(\(3\))と式(\(4\))と同様に次のようなTaylor展開を考えます。 \[f(x+h) = f(x) + f'(x)h + \frac{1}{2}f''(x)h^2 + \frac{1}{6}f^{(3)}(x)h^3 + O(h^4), \tag{6}\] \[f(x-h) = f(x) - f'(x)h + \frac{1}{2}f''(x)h^2 - \frac{1}{6}f^{(3)}(x)h^3 + O(h^4), \tag{7}\] さらに、式(6)と式(7)を用いることで、次のような関係式を導くことが出来ます。 \[f(x+h) -2 f(x) +f(x-h) = f''(x)h^2 +O(h^4). \tag{8} \] さらに式変形を行うことで、次のような式を得ることができます。 \[f''(x) = \frac{f(x+h) -2 f(x) +f(x-h)}{h^2} +O(h^2). \tag{9} \] この式は、2階微分の差分公式で、2階微分を数値的に評価する際に用います。また、右辺最後の\(O(h^2\))より、差分公式の誤差が\(h^2\)に比例することが分かります。

ここでは例題として、三角関数\(f(x)=\sin(x)\)の二階微分を数値的に計算するプログラムを見てみます。三角関数は解析的に微分でき、関数\(f(x)=\sin(x)\)の2階微分は\(f''(x)=-\sin(x)\)となります。この微分を数値的に評価するために、差分公式、式(7)を用いてるプログラムを考えます。ここでは、三角関数の1周期である(\( 0\le x \le 2 \pi \))に渡って二階部分を評価します。

(lesson1_2.f90)

program main
  implicit none
  integer :: i, n
  real(8) :: ff_0, ff_p, ff_m, d2fdx2
  real(8) :: x, h, x_i, x_f


  x_i = 0d0
  x_f = 2d0*3.14159d0
  
  n = 100
  h = (x_f - x_i)/n

  
  open(20,file="second_order_derivative_sin.out")
! second order derivative of sin(x)  
  do i = 0, n
     x = x_i + i*h

     ff_0 = sin(x)
     ff_p = sin(x+h)
     ff_m = sin(x-h)
     d2fdx2 = (ff_p - 2d0*ff_0 + ff_m)/h**2

     write(20,"(3e16.6e3)")x,d2fdx2,-sin(x)
  end do
  close(20)
  
end program main

上のコードでは、三角関数\(f(x)=\sin (x)\)の2階微分が範囲\(0 \le x \le 2\pi\)に渡って評価しています。ここでは、評価範囲の始点をx_i = 0d0で設定し、終点をx_f = 2d0*3.14159によって設定しています。ここで、3.14159は円周率\(\pi\)の近似値です。次に、評価区間であるx_iとx_fの間の区間をnの小区間に分割します。この際、小区間の幅\(h\)は次式で表されます:h = (x_f - x_i)/n. 上のコードのdoループ内では、二階微分の値が差分公式, 式(\(7\)),により評価され、出力ファイルsecond_order_derivative_sin.outに書き出されます。この出力ファイルの3列目には、三角関数の2階微分の解析的な評価値である-sin(x)の値も一緒に出力されています。

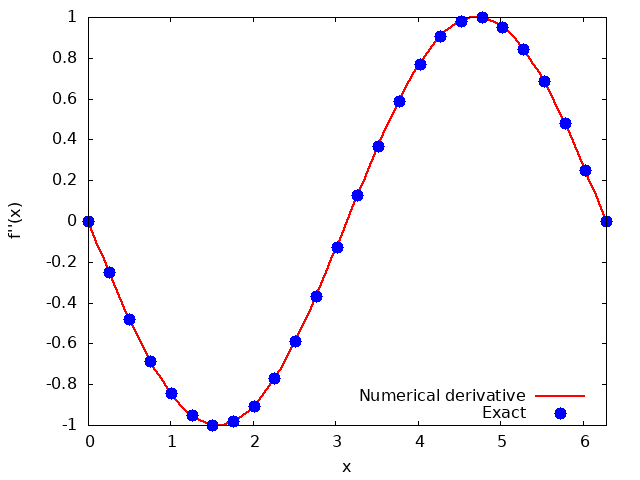
下の図では、上記のプログラムによって出力されたsecond_order_derivative_sin.outの結果を図示して、2階微分を差分法によって評価した値と厳密な値を比較している。数値微分によって、厳密な微分の値を再現できていることが確認できている。