Lesson 1: 数値微分

Lesson 1-1: 差分法 (前進差分)

数値的に微分を行う方法を考えるために、まずは微分の数学的定義を復習してみましょう。関数\(f(x)\)の微分は以下のように定義されます。 \[f'(x)=\lim_{h\rightarrow 0} \frac{f(x+h)-f(x)}{h}.\]

この微分の定義を用いて、十分に小さい幅\(h\)を使って関数\(f(x)\)の微分\(f'(x)\)を以下のように近似することを考えます。 \[ f'(x)\approx \frac{f(x+h)-f(x)}{h}. \tag{1}\] このように、有限の幅\(h\)を使った微分の近似を有限差分近似、または単に差分近似と呼びます。特に、式(1)のような関数を前方に移動させた値\(f(x+h)\)を用いた近似式を前進差分公式と呼びます。

差分近似のの精度を検証するために、式(1)を使用して関数\(f(x)=e^x\)の\(x=1\)における微分を評価し、正確な値\(f'(1)=e^1=e\)と比較してみましょう。以下にソースコードを見てみましょう。

(lesson1_1.py)

 import numpy as np
 
 x = 1.0
 h = 0.1
 
 f0 = np.exp(x)
 fp = np.exp(x+h)
 
 dfdx = (fp-f0)/h
 
 print('h=',h)
 print('dfdx=',dfdx)
 print('Error=',dfdx-np.exp(1.0))

以下に、上のソースコードの概要について解説します。最初の行でimport numpy as npを使用してnumpyのモジュールをインポートして、numpyの数学関数を使う準備をしています。ここでインポートの際にas npを追加するこで、numpyの短縮名npを定義し、numpyをnpとして呼び出せるようにしています。

コードの3行目と4行目では、\(x=1\)における微分値をステップ幅\(h=0.1\)を用いて差分公式(1)で評価するため、x = 1.0とh = 0.1によって値を設定しています。

コードの6行目と7行目では、numpyの指数関数np.exp()を使用して\(x\)と\(x+h\)での関数の値が計算され、それぞれ変数f0とfpに格納しています。9行目では前進差分公式、式(1)、を使用して微分値を近似的に評価しています。また、12行目と13行目では、上記の計算により得られた微分の近似値と、正確な微分値との差異が出力されます。

上記プログラムを実行して、微分が差分近似によってうまく近似されているかを確認しましょう。また、ステップ幅\(h\)を変更することで近似の精度がどのように変わるかも確認しましょう。

Lesson 1-2: 差分近似とその誤差 (中心差分近似)

前節では、微分を近似する方法として有限差分法を学びました。微分の定義より、幅\(h\)が小さくなる極限で近似が厳密になるので、近似の誤差も幅\(h\)と共に小さくなることが期待されます。

ここでは、この誤差の大きさをテイラー展開(Taylor展開)を用いて評価してみましょう。まず、次のようなテイラー展開を考えます: \[f(x+h)=f(x)+f'(x)h+\mathcal{O}(h^2). \tag{2}\] ここで、\(O(h^2)\)は、\(h\)の2次以上の項からなり、テイラー展開を有限の次数で打ち切った誤差を表しています。式(2)を変形することで次のような式を得ることができます。 \[f'(x)=\frac{f(x+h)-f(x)}{h}+\mathcal{O}(h).\]

したがって、前進差分公式(1)の誤差は\(\mathcal{O}(h)\)であり、\(h\)が小さい極限で近似の誤差は\(h\)に比例します。

また、テイラー展開を用いることで、より高精度な差分近似公式を作ることが出来ます。ここでは、以下のように2つのテイラー展開を考えてみましょう: \[ f(x+h)=f(x)+f'(x)h+\frac{1}{2}f''(x)h^2 + \mathcal{O}(h^3),\] \[ f(x-h)=f(x)-f'(x)h+\frac{1}{2}f''(x)h^2 + \mathcal{O}(h^3).\] これら2つの式の差を取る\(h^2\)で割ることで、次のような差分公式を作ることが出来ます。 \[ f'(x)=\frac{f(x+h)-f(x-h)}{2h}+\mathcal{O}(h^2). \tag{3} \] この差分公式は中心差分公式と呼ばれ、正と負の方向に対称的に差分を取ります。誤差項は\(\mathcal{O}(h^2)\)であり、\(h^2\)のオーダーの誤差があることを示しています。

これは、\(h\)が小さくなる極限で、全身差分近似公式[式(1)]に比べて中心差分近似公式[式(3)]が急速に誤差が小さくなることを意味しています。

前進差分公式と中心差分公式の精度が刻み幅 \(h\) に対してどのように振る舞うかを実際のプログラムを書いて検証してみましょう。上記の例と同様に、関数 \(f(x)=e^x\) の \(x=1\) における導関数値を見つけるPythonプログラムが以下に示します。

(lesson1_2.py)

 from matplotlib import pyplot
 import numpy as np
 
 
 # Compute the derivative with the forward difference
 def fdiff_forward(x,h):
     fx = np.exp(x)
     fx_ph = np.exp(x+h)
     dfdx = (fx_ph-fx)/h
     return dfdx
 
 # Compute the derivative with the central difference
 def fdiff_central(x,h):
     fx_ph = np.exp(x+h)
     fx_mh = np.exp(x-h)
     dfdx = (fx_ph-fx_mh)/(2.0*h)
     return dfdx
 
 # set the numerical parameters
 x = 1.0
 n = 16
 
 # define the arrays
 h = np.zeros(n)
 dfdx_f = np.zeros(n)
 dfdx_c = np.zeros(n)
 
 for i in range(n):
     h[i] = 0.8**i
     dfdx_f[i] = fdiff_forward(x,h[i])
     dfdx_c[i] = fdiff_central(x,h[i])
 
 # evaluate the error
 error_f = np.abs(dfdx_f - np.exp(x))
 error_c = np.abs(dfdx_c - np.exp(x))
 
 
 # Plot the date
 pyplot.plot(h, error_f, label="Forward difference")
 pyplot.plot(h, error_c, label="Central difference")
 
 pyplot.xscale('log')
 pyplot.yscale('log')
 
 pyplot.xlabel('h')
 pyplot.ylabel('Error')
 pyplot.legend()
 
 pyplot.savefig("error_derivative.png")
 pyplot.show()

それでは、上記のPythonプログラムを見てみましょう。

5行目は、#で始まるコメント行で、プログラム上では何も作用しませんが、プログラムを読む人の理解を助けるために書かれる行です。6行目は、def文によって手続きfdiff_forward(x,h)を定義しています。このようにdef文で定義された手続きは、プログラム内から呼び出すことができます。また、この手続きを表すブロックはインデント(字下げ)によって表されます。この6行目で定義された関数fdiff_forward(x,h)は、前方差分公式(1)を使って関数の微分値を計算する関数です。

また、13行目から定義される関数fdiff_central(x,h)は、中心差分公式(3)によって微分値を計算する関数です。

24行目では、変数hはサイズnのnumpy配列（numpyモジュールで定義された配列）として初期化されます。ここで使用されている関数np.zerosは、全ての要素に0を割り当てることで配列を初期化する関数です。同様に、25,26行目で関数の微分値を計算した値を保存するための配列dfdx_fとdfdx_cもnumpy配列として初期化しています。

28行目から始まるforループでは、刻み幅h[i]を小さくしながら、上で定義された関数fdiff_forwardとfdiff_centralを用いて、前方差分法と中心差分法によって関数の微分値を計算していきます。

34行目と35行目では、微分の厳密な値(np.exp(x))と上記のforループ内で計算された微分の近似値の差を取ることで、差分近似の誤差を計算しています。

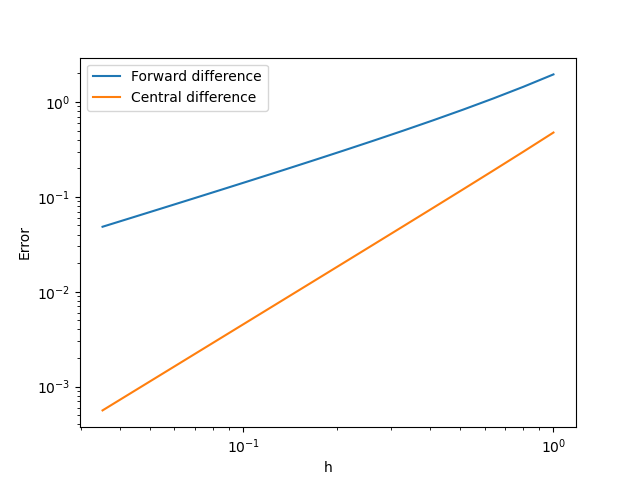
コードの38行目以降では、上記で計算した差分近似の誤差を刻み幅(\(h\))の関数として図示しています。ここでは、両対数グラフを用いていることに注意してください。

図を見ると、前方差分近似（青線）の誤差が\(h\)に比例しているのに対して、中心差分近似（オレンジ線）の誤差が\(h\)の2乗に比例していることがわかります。この振る舞いは、上で議論したテイラー展開を用いた誤差解析と整合した結果となっています。

Lesson 1-3: 2階微分の数値微分

前節では、差分近似によって1階微分を数値的に評価しました。この節では、1階微分の数値計算で得た知識を応用して、2階微分を数値的に評価する方法を学びます。

次のようなテイラー展開を考えてみましょう: \[ f(x+h)=f(x)+f'(x)h+\frac{1}{2}f''(x)h^2+\frac{1}{6}f^{(3)}(x)h^3 + \mathcal{O}(h^4),\] \[ f(x-h)=f(x)-f'(x)h+\frac{1}{2}f''(x)h^2-\frac{1}{6}f^{(3)}(x)h^3 + \mathcal{O}(h^4).\] この二つのテイラー展開の和から\(2f(x)\)を引くことで、次のような2階微分の差分近似公式を作ることが出来ます。 \[ \frac{d^2f(x)}{dx^2}=\frac{f(x+h)-2f(x)+f(x-h)}{h^2}+\mathcal{O}(h^2). \] したがって、1階微分の場合と同様に、差分近似を用いて2階微分の値を数値的に評価することができます。また、この差分公式の誤差のオーダーは\(\mathcal{O}(h^2)\)です。

以下のPythonコードは、関数\(f(x)=\cos(x)\)の二階微分\(f''(x)\)を数値的に計算するプログラムを示しています。二階微分とPythonプログラムに慣れるために、同様のコードを自作してみましょう。

(lesson1_3.py)

 from matplotlib import pyplot
 import numpy as np
 
 def second_order_derivative_cos(x,h):
     fx = np.cos(x)
     fx_ph = np.cos(x+h)
     fx_mh = np.cos(x-h)
     d2fdx2 = (fx_ph -2*fx +fx_mh)/h**2
     return d2fdx2
 
     
 h = 0.1
 nx = 52
 xini = 0.0
 xfin = 7.0
 
 x = np.linspace(xini, xfin, nx)
 fx = np.cos(x)
 
     
 d2fdx2 = second_order_derivative_cos(x,h)
 
 
 pyplot.plot(x, fx, label="f(x)=cos(x)")
 pyplot.plot(x, d2fdx2, label="f''(x)")
 
 pyplot.xlabel('x')
 pyplot.ylabel('f(x)')
 pyplot.legend()
 pyplot.savefig("second_derivative_cos.png")
 pyplot.show()

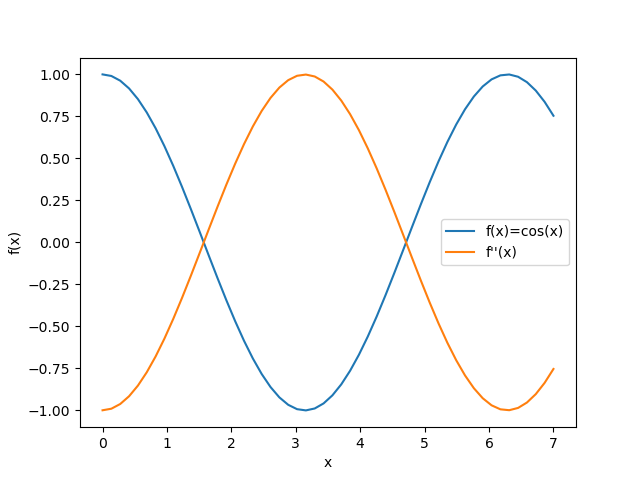
下の図は、上記のサンプルコードを実行することで得られる、\( f(x)=\cos(x) \) と \(f''(x) \) を図示したものです。