Lesson 2: 数値積分

Lesson 2-1: 台形公式と数値積分

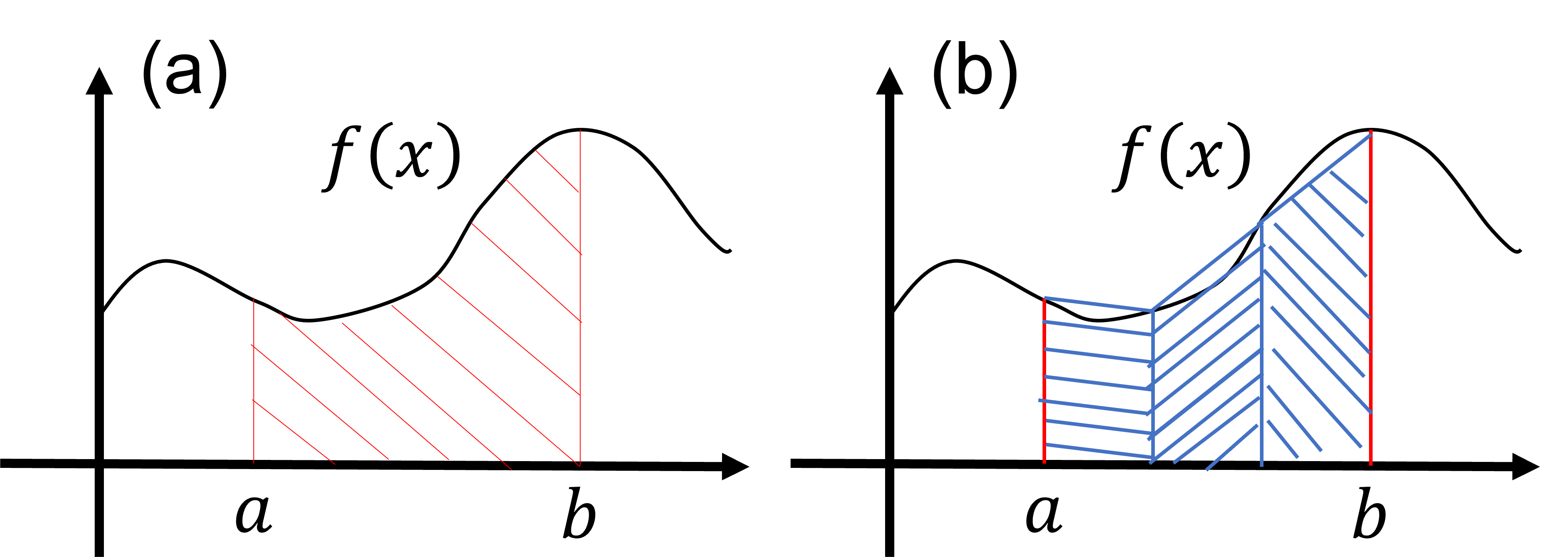
数値的に積分を評価するために、まずは積分について復習してみましょう。ここでは、次のような関数\(f(x)\)の積分を考えます: \[ S=\int^b_a dx f(x). \tag{1} \] 式(1)の積分の値\(S\)は下図(a)の赤斜線で塗られた部分の面積に等しいことが知られています。この事実に基づき、式\((1)\)の積分値を複数の台形の面積の和として近似することが出来ます。例えば、下図(a)の赤斜線で塗られた部分の面積は、下図(b)の青斜線で塗られた3つの台形の面積の和として近似することを考えます。もし、積分区間\((a\le x \le b)\)が等しい幅を持った3つの領域に分割されていると仮定すると、下図(b)の3つの台形の面積による積分の近似値は次のように求めることが出来ます: \[ h = \frac{b-a}{3}, \tag{2} \] \[ S_3=\frac{f(a)+f(a+h)}{2}h+\frac{f(a+h)+f(a+2h)}{2}h +\frac{f(a+2h)+f(b)}{2}h. \tag{3} \] ここで\(h\)は分割された区間の幅を表し、\(S_3\)は下図(b)の青斜線の領域の面積を表しています。この式は、さらに次の式のように書き換えることが出来ます: \[ S_3=h \times \left [ \frac{f(a)}{2}+f(a+h)+f(a+2h) + \frac{f(b)}{2} \right ]. \tag{4} \] この表式は、次に見るようなより多くの台形による積分の近似式を作るのに便利な形をしています。

上の議論では、式(\(1\))の積分値を式(\(4\))の3つの台形を用いた近似式で評価することを考えました。上図(b)から期待されるように、分割する区間を増やし、より多くの台形を用いて面積を近似した方が、より正確に積分値を近似することが出来ます。例えば、もし積分区間\((a\le x \le b)\)を\(N\)個の小区間に分割し、それぞれの小区間の積分値を台形の面積で近似した場合、\(N \)の台形の面積の和による積分の近似値は次のように表すことが出来ます: \[ h = \frac{b-a}{N}, \tag{5} \] \[ x_n = a + n\times h ~~~\rm{for}~~~ (0\le n \le N), \tag{6} \] \[ S_n = h\times \left [\frac{f(x_0)}{2} +f(x_1)+\cdots+f(x_{N-1})+\frac{f(x_N)}{2} \right ] \tag{7}. \] ここで\(h\)は分割された小区間の幅を表し、\(x_n\)は\(n\)番目のグリッド点の座標を表しています。また、\(n\)は\(0\)と\(N\)の間の整数を表します。この式(\7\))では、式(\(1\))の積分値が\(N\)個の台形の面積によって近似されています。

式(\(7\))の積分の近似公式は台形公式(trapezoidal rule)として知られており、分割数\(N\)が大きい極限(\(N \rightarrow \infty\))で厳密な積分値を与える公式となっています。

Lesson 2-2: 台形公式を使ったFotranコードの書き方

ここでは、台形公式（式 (\(7\))）を用いて数値的に次の積分を評価します： \[ \int_0^1 dx \frac{4}{1+x^2}=\pi \tag{8}. \] 下記のコードでは、積分領域（\(0\le x \le 1\))を\(N=20\)の台形に分割し、積分を評価しています。また、コードの解説を、コードの下に示しましたので参考にしてください。

(lesson2_1.f90)

program main
  implicit none
  integer :: i, n
  real(8) :: a, b
  real(8) :: x, h, f, s


  n = 20

  a = 0d0
  b = 1d0
  h = (b-a)/n

  x = a
  f = 4d0/(1d0+x**2)
  s = 0.5d0*h*f
  do i = 1, n-1

     x = a + h*i
     f = 4d0/(1d0+x**2)
     s = s + h*f

  end do
  x = b
  f = 4d0/(1d0+x**2)
  s = s + 0.5d0*h*f

  write(*,*)"Result:"
  write(*,"(es26.16e3)")s
  
end program main

上記のFortranコードでは、8行目のn=20で、格子点の数を20に設定しています。次に、10行目、11行目で次のように積分範囲を定義しています:

a = 0d0
b = 1d0 

その後、12行目で台形の幅を

h = (b-a)/n

で計算します。

14行目からのブロックでは、次のように変数 s に関数の値を足していくことによって、台形公式（式 (\(7\))）により積分を評価しています:

  x = a
  f = 4d0/(1d0+x**2)
  s = 0.5d0*h*f
  do i = 1, n-1

     x = a + h*i
     f = 4d0/(1d0+x**2)
     s = s + h*f

  end do
  x = b
  f = 4d0/(1d0+x**2)
  s = s + 0.5d0*h*f

最後に、以下のブロックで結果が出力されます：

  write(*,*)"Result:"
  write(*,"(es26.16e3)")s

結果は\(\pi=3.14159...\)に近いですか？上記のコードでは、nを大きな値に設定することで、より正確な値を得ることができます。nの関数としての誤差がどのように振る舞うかを確認しましょう。