Lesson 3:
1階常微分方程式の数値解法

Lesson 3-1: オイラー法 (Euler法)

まず初めに、オイラー法 (Euler法)と呼ばれる最もシンプルな計算方法について学びます。オイラー法について解説するために、関数の微分について復習してみましょう。ある関数 \(y(x)\)の微分は次のように定義されています。: \[ \frac{dy(x)}{dx}=\lim_{\Delta x \rightarrow 0}\frac{y(x+\Delta x)-y(x)}{\Delta x}. \tag{2} \] この定義をもとに、十分小さな\(\Delta x\)を用いて微分を近似することを考えます。このような近似を差分近似と呼びます。差分近似については、数値微分の解説も参考にしてみてください。式(\(2\))を差分近似すると次のような近似式を得ることが出来ます: \[ \frac{dy(x)}{dx}\approx \frac{y(x+\Delta x)-y(x)}{\Delta x}. \tag{3} \] この近似式(\(3\))は極限\(\Delta x \rightarrow 0\)において厳密になります。この式(\(3\))を常微分方程式(\(1\))に代入することで、次のような常微分方程式の差分近似式を作ることが出来ます。 \[ y(x+\Delta x)=y(x)+\Delta f\left ( x,y(x) \right ). \tag{4} \] この差分近似方程式(\(4\))がオイラー法を用いて微分方程式を解く際に中心的な役割を果たします。以下で解説するように、この式(\(4\))を繰り返し用いることで、関数\(y(x)\)の値を逐次的に求めていくことが出来ます。

Lesson 3-2: オイラー法(Euler法)の具体的な手順

ここでは、オイラー法を用いて微分方程式を解いていく実際の過程について見ていきます。例として、微分方程式(\(1\))を初期条件\(y(x_0)=y_0\)の元で解くことを考えます。まず、式(\(4\))を一度 \( (x_0,y_0)\)において用いることで、次式を得ます。 \[ y(x_0+\Delta x)=y_0 + \Delta x f(x_0,y_0). \tag{5} \] ここで\(x_1 = x_0+\Delta x\)と \(y_1 = y(x_0+\Delta x)=y(x_1)\)とします。ここで、さらに式(\(4\))を用いることで次式を得ます。 \[ y(x_1+\Delta x)=y_1 + \Delta x f(x_1,y_1). \tag{6} \] さらに\(x_2 = x_1+\Delta x\)と\(y_2 = y(x_1+\Delta x)=y(x_2)\)とします。このような操作を繰り返すことで、あるデータ点\( (x_n, y_n)\)に対して次のような漸化式を得ることが出来ます。 \[ y_n = y_{n-1} + \Delta x f(x_{n-1},y_{n-1}). \tag{7} \] この方法はオイラー法(Euler法)として知られている方法で、最もシンプルな微分方程式の数値解法です。下図にはこのオイラー法を用いて微分方程式を逐次的に解いていく過程が示されています。

Lesson 3-3: オイラー法のFortranコードの書き方

次に、オイラー法を用いて1階の常微分方程式を解くためのFortranコードの書き方について学びます。ここでは例として、次の微分方程式を解くことを考えます: \[ \frac{dy}{dx}=(y-1)y. \tag{8} \] 初期条件として\( y(0)=\frac{1}{10}\)とします。この微分方程式は解析的に解くことか可能で、その解析解は次のようになります。 \[ y(x)=\frac{e^x}{9+e^x}. \tag{9} \] この式(\(9\))を式(\(8\))に代入することで、微分方程式の解になっていることを確かめることが出来ます。

以下のプログラム例では、微分方程式(\(8\))をオイラー法を用いて解いています。このプログラムに関する解説は、コードの下に示してあるので参考にしてください。。

(lesson3_1.f90)

program main
  implicit none
  integer :: n, i
  real(8) :: x, f, y, y_new, dx, xf

  n = 8
  xf = 10d0
  dx = xf/n

  open(20,file="result_Euler.out")

  x = 0d0
  y = 1d0/10d0
  write(20,"(2e16.6e3)")x,y


  do i = 0, n-1

     x = dx*i
     f = (1d0-y)*y
     y_new = y + dx*f

     x = dx*(i+1)

     write(20,"(2e16.6e3)")x,y_new

     y = y_new

  end do

  close(20)

end program main

上記のコードでは範囲(\(0\le x \le 10\))を8点に分割してオイラー法を用いて微分方程式を解いています。これを実現するために、コードの6行目でn=8によって分割数を指定し、また7行目でxf = 10d0で微分方程式を解く終点を指定しています。これらの情報から、8行目で分割の刻み幅dxをdx=xf/nによって計算しています。

コードの10行目ではopen(20,file="result_Euler.out")によってresult_Euler.outというファイルを開き、オイラー法の計算結果を出力するための準備を行っています。

コードの12,13行目では\(y(0)=0\)の初期条件を設定し、13行目ではx=0におけるyの値をファイルresult_Euler.outへ出力しています。

コード17行目からのDOループでは、オイラー法の公式、式(7)、を用いて微分方程式の求解を行っています。まず、19,20行目でi番目のx座標(x_i)における関数fの値を求め、21行目で(i+1)番目のx座標におけるyの値(y_i+1)を式(7)によって求めています。さらに、25行目ではここで求めた(i+1)番目の値(x_i+1, y_i+1)をwrite文でファイルに出力しています。

DOループの最後で、y=y_newによって、新しく求めたyの値(y_new)を変数yに代入し、DOループの先頭に戻ります。このような手続きを繰り返し行うことによって、逐次的に微分方程式を解いていくことが出来ます。

コードの最後のclose(20)によって、ファイル"result_Euler.out"を閉じてプログラムを終了します。

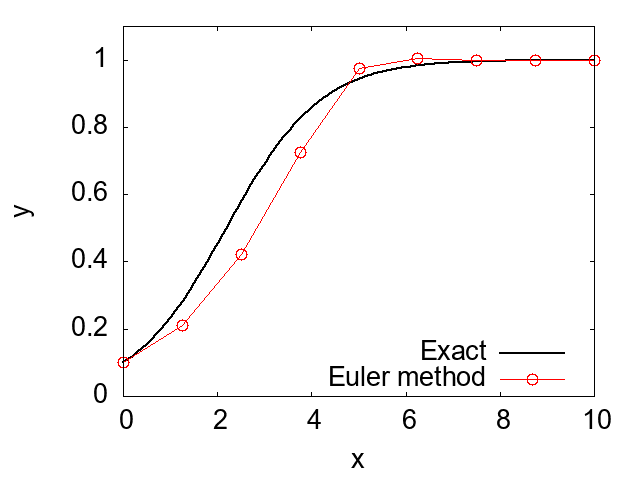
下図には、上記のオイラー法のプログラムによって得られた数値解(赤線: Euler method)と解析解(黒線: Exact)を示しました。オイラー法の数値解と解析解の間に誤差があることが確認できます。このオイラー法の誤差は差分近似に由来するものであり、より小さい刻み幅を用いることで誤差を低減することが可能です。

しかしながら、高精度の解を得るために非常に小さな刻み幅を用いえると、それに伴い計算コストが増大してしまいます。小さな刻み幅を用いる代わりに、より洗練されたアルゴリズムを用いることで数値解の精度を高めることも可能です。次の節では、予測子-修正子法と呼ばれるオイラー法の改良したアルゴリズムについて学びます。

Lesson 3-4: 予測子・修正子法

上の例でみたように、オイラー法を用いて微分方程式を数値的に解くことが可能ですが、その精度は実用の計算には不十分であることが多いです。ここでは、オイラー法よりも高精度な方法として予測子・修正子法について学びます。式(3)をよく見ると、オイラー法は前進差分法に基づいていることが分かります。そこで、ここでは前進差分よりも精度の高い中心差分に基づいたアルゴリズムを作ることを考えてみましょう。

中心差分を用いた微分の近似公式は次のようになります: \[ \frac{dy \left (x +\frac{\Delta x}{2} \right )}{dx} \approx \frac{y(x+\Delta x) -y(x)}{\Delta x} \tag{10} \]

この式(10)を用いることで、微分方程式(1)を次のように近似することが出来ます。 \[ \frac{y(x+\Delta x) -y(x)}{\Delta x} \approx \frac{dy \left (x +\frac{\Delta x}{2} \right )}{dx} = f\left ( x+\frac{\Delta x}{2},y \left (x+\frac{\Delta x}{2} \right ) \right) \tag{11} \].

ここでさらに、式(11)の右辺を\(x\)と\(x+\Delta x \)の二点での関数fの値の平均値として近似することを考えます。 \[ f\left ( x+\frac{\Delta x}{2},y \left (x+\frac{\Delta x}{2} \right ) \right) \approx \frac{f\left (x,y(x) \right) +f\left (x+\Delta x,y(x+\Delta x) \right) }{2} \tag{12} \]

式(12)を式(11)へ代入し整理することで、次のような方程式を導くことが出来ます。 \[ y(x+\Delta x)= y(x) + \frac{\Delta x}{2} \left [ f\left (x,y(x) \right) +f\left (x+\Delta x,y(x+\Delta x) \right) \right ] \tag{13} \] この式(\(13\))は予測子・修正子法において中心的な役割を果たします。また、この式(\(13\))は中心差分近似に基づいているため、前進差分近似に基づくオイラー法よりも高精度な近似式となっています。

原理的には式(13)を用いることで、微分方程式(1)を数値的に解くことが出来ますが、実際にこの方程式を用いたコードを書こうとするとある問題が生じます。それは、式(13)の左辺である\(y(x+\Delta)\)を求めるためには、その\(y(x+\Delta)\)自身の値を右辺で用いなければいけないという問題です。

このように、式(13)を用いて\(y(x+\Delta)\)の値を求めるためには、予めその値を知っていなければならない。この式(13)の性質はオイラー法の公式[式(4)]の性質とは全く異なります。オイラー法の公式[式(4)]の場合は、右辺は既知の量だけで記述されているのでオイラー法によって\(y(x+\Delta x) \)の値を求める際には特に問題はありませんでした。

実際に式(13)を用いて数値計算を行う場合は、式(13)を厳密に用いる代わりに、式(13)を近似的に評価して微分方程式を数値的に求解します。この近似手法を導くために、次のような2段階のステップを考えてみましょう(この手法は予測子・修正子法と呼ばれる)。

まず、第一段階目のステップとして、\(y(x+\Delta x)\)の値をオイラー法によって次のように予測します。 \[ y^{\rm{pred}}(x+\Delta x)=y(x)+f(x,y(x))\Delta x. \tag{14} \]

次に、二段階目のステップ(修正ステップ)として、予測ステップによって得られた値\(y^{\rm{pred}}(x+\Delta x)\)を、式(13)の右辺の\(y(x+\Delta x)\)の値の近似値として用います: \[ y(x+\Delta x)= y(x) + \frac{\Delta x}{2} \left [ f\left (x,y(x) \right) +f\left (x+\Delta x,y^{\rm{pred}}(x+\Delta x) \right) \right ]. \tag{13} \]

このように、予測子・修正子法では予測と修正の二つのステップを用いて式(13)を近似的に評価します。

予測子・修正子法の精度を確認するために、式(8)の微分方程式を予測子・修正子法によって解き、上で議論したオイラー法での結果と比較してみよう。この比較を行うための、予測子・修正子法のプログラム例を以下に示します。

(lesson3_2.f90)

program main
  implicit none
  integer :: n, i
  real(8) :: x, f, y, y_new, dx, xf
  real(8) :: y_exact
  real(8) :: y_pred, f_pred


  n = 8
  xf = 10d0
  dx = xf/n

  open(20,file="result_PredictorCorrector.out")

  x = 0d0
  y = 0.1d0
  y_exact = exp(x)/(9d0+exp(x))
  write(20,"(3e16.6e3)")x,y,y_exact


  do i = 0, n-1

     x = dx*i
     f = (1d0-y)*y
     y_pred = y + dx*f

     f_pred = (1d0-y_pred)*y_pred
     y_new = y + dx*0.5d0*(f + f_pred)

     x = dx*(i+1)
     y_exact = exp(x)/(9d0+exp(x))

     write(20,"(3e16.6e3)")x,y_new,y_exact

     y = y_new

  end do

  close(20)

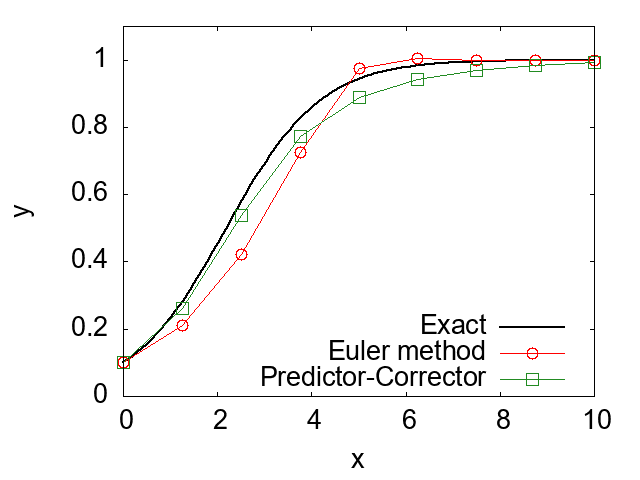
end program main

上記のコードを用いることで、微分方程式(8)の数値解を得ることが出来る。下図に、予測子・修正子法によって得られた結果とオイラー法によって得られた結果、及び解析解の比較を示します。ここでは、オイラー法と予測子・修正子法は同じ刻み幅\(\Delta x \)を用いています。図を見てわかるように、予測子・修正子法がオイラー法よりも正確な数値解を与えていることを確認できます。練習問題として、上記のプログラムにおける刻み幅を増減させながら、予測子・修正子法と解析解の差がどのように変化するか観察してみよう。

Lesson 3-5: ルンゲクッタ(Runge-Kutta)法

前節で学んだ予測子・修正子法は、2段階のステップを踏むことでオイラー法よりも精度の高い精度で数値解を求める方法でした。この考えを拡張することで、多段階のステップを踏むことでより高精度なアルゴリズムを考えることも可能です。最も良く用いられる高精度のアルゴリズムはルンゲクッタ(Runge-Kutta)法と呼ばれるものです。

ルンゲクッタ法は、次のような4段階の過程を踏むことで、4点の微分値,\(\frac{dy(x)}{dx} =f\left (x,y(x) \right )\),を計算し、そこから次のyの値(\(y(x+\Delta x)\))を求める方法となります。ルンゲクッタ法のアルゴリズムを理解するために、オイラー法を多段階法の観点からオイラー法を振り返ってみましょう。

　多段階法の観点から見ると、オイラー法は\(y(x+\Delta x)\)の値を次のような1段階のステップでの求める方法であると考えることが出来ます: \[ k_1 = f(x, y(x)), \tag{15} \] \[ y(x+\Delta x) = y(x) + k_1 \times \Delta x . \tag{16} \] この式(15),及び式(16)は上で述べたオイラー法[式(4)]と等価の式となっています。

　ルンゲクッタ法は、上記のオイラー法を4段階のステップに拡張したものとみなすことができ、次のようなアルゴリズムで\(y(x+\Delta x)\)の値を求める方法です: \[k_1 = f \left (x, y(x) \right ), \tag{17}\] \[k_2 = f\left (x+\frac{\Delta x}{2}, y(x)+ \frac{\Delta x}{2} k_1 \right ), \tag{18}\] \[k_3 = f\left (x+\frac{\Delta x}{2}, y(x)+ \frac{\Delta x}{2} k_2 \right ), \tag{19} \] \[k_4 = f\left (x+\Delta x, y(x)+k_3 \Delta x \right ), \tag{20}\] \[y(x+\Delta x) =y(x) + \Delta x \times \frac{k_1 + 2k_2 + 2k_3 + k_4}{6}. \tag{21} \] これらの式(17-21)を用いることで、高精度で微分方程式を解くのが(4次の)ルンゲクッタ法です。

下記のプログラム例は、ルンゲクッタ法を用いて微分方程式(8)を数値的に解くものです。

(lesson3_3.f90)

program main
  implicit none
  integer :: n, i
  real(8) :: x, f, y, y_new, dx, xf
  real(8) :: y_exact
  real(8) :: k1,k2,k3,k4,y_tmp


  n = 8
  xf = 10d0
  dx = xf/n

  open(20,file="result_RungeKutta.out")

  x = 0d0
  y = 0.1d0
  y_exact = exp(x)/(9d0+exp(x))
  write(20,"(3e16.6e3)")x,y,y_exact


  do i = 0, n-1

     x = dx*i

     k1 = (1d0-y)*y

     y_tmp = y+0.5d0*dx*k1
     k2 = (1d0-y_tmp)*y_tmp

     y_tmp = y+0.5d0*dx*k2
     k3 = (1d0-y_tmp)*y_tmp

     y_tmp = y+dx*k3
     k4 = (1d0-y_tmp)*y_tmp

     y_new = y + (dx/6d0)*(k1+2d0*k2+2d0*k3+k4)

     x = dx*(i+1)
     y_exact = exp(x)/(9d0+exp(x))

     write(20,"(3e16.6e3)")x,y_new,y_exact

     y = y_new

  end do

  close(20)

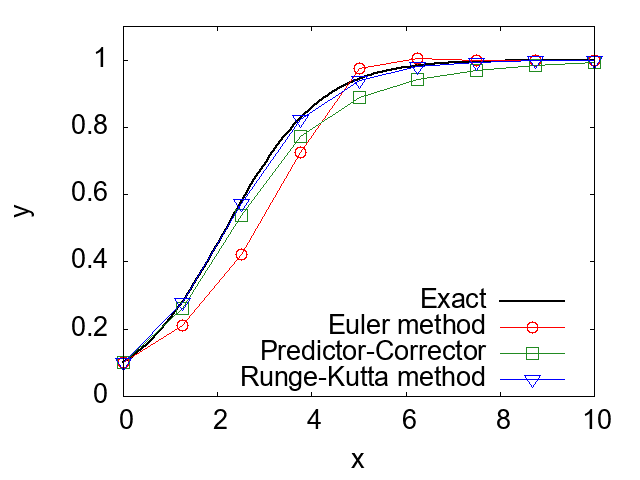
end program main

上記のプログラムを用いることで、微分方程式(8)を数値的に解くことが出来ます。下図には、Runge-Kutta法によって得られた数値解を予測子・修正子法、オイラー法、解析解によって得られる結果と比較したものが示しました。図から分かるように、Runge-Kutta法が非常に正確に微分方程式を求解していることが確認できます。