Pythonで数値積分: 台形公式

このページでは、Pythonを用いて数値的に積分を評価する数値積分について学びます。

Lesson 2-1: 台形公式と数値積分

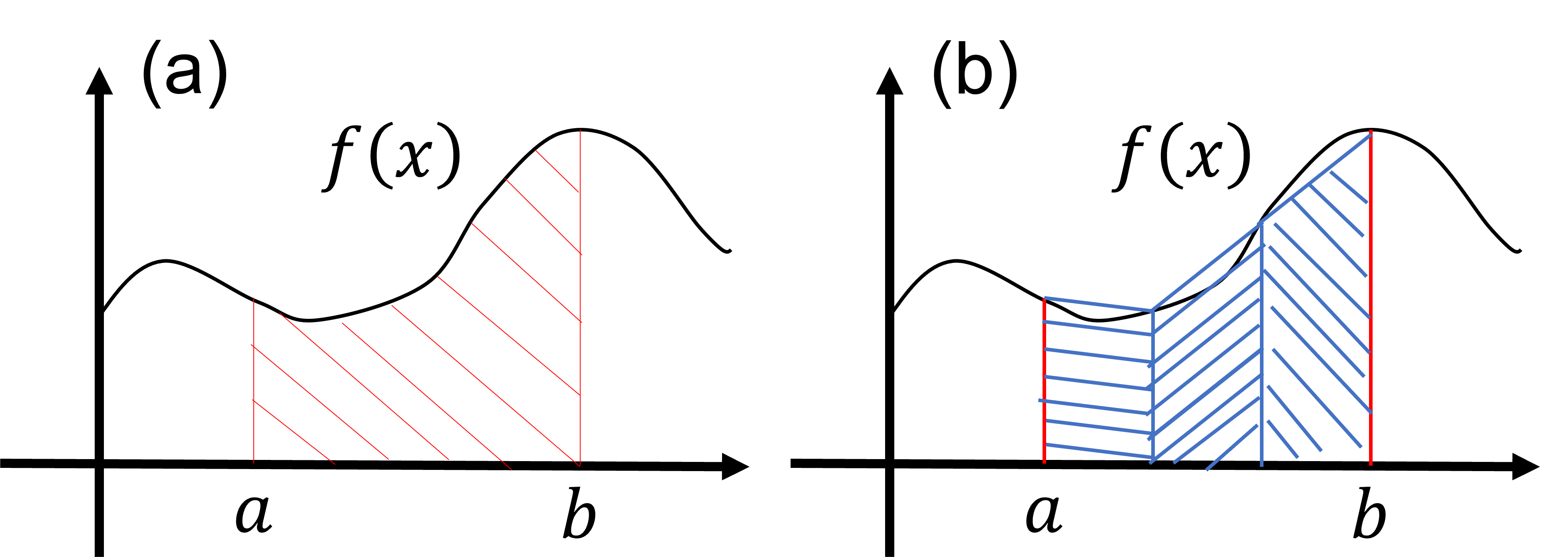
この節では、関数の積分を数値計算で評価する数値積分について学びます。まず、次のような関数\(f(x)\)の積分を考えてみましょう： \[ S=\int^{b}_{a} dx f(x). \tag{1} \] 式(1)の積分の値\(S\)は下図(a)の赤斜線で塗られた部分の面積に等しいです。

この事実に基づき、式(1)の積分を、複数の台形の和として近似することを考えます。例として、下図(a)の赤斜線で塗られた部分の面積は、下図(b)の青斜線で塗られた3つの台形の面積の和として近似することを考えます。

もし、積分区間\((a\le x \le b)\)が等しい幅を持った3つの領域に分割されていると仮定すると、下図(b)の3つの台形の面積による積分の近似値は次のように求めることが出来ます: \[ h = \frac{b-a}{3}, \tag{2} \] \[ S_3=\frac{f(a)+f(a+h)}{2}h+\frac{f(a+h)+f(a+2h)}{2}h +\frac{f(a+2h)+f(b)}{2}h. \tag{3} \] ここで\(h\)は分割された区間の幅を表し、\(S_3\)は下図(b)の青斜線の領域の面積を表しています。この式は、さらに次の式のように書き換えることが出来ます: \[ S_3=h \times \left [ \frac{f(a)}{2}+f(a+h)+f(a+2h) + \frac{f(b)}{2} \right ]. \tag{4} \] この表式は、次に見るようなより多くの台形による積分の近似式を作るのに便利な形をしています。

上の議論では、式(1)の積分値を式(4)の3つの台形を用いた近似式で評価することを考えました。上図(b)から期待されるように、分割する区間を増やし、より多くの台形を用いて面積を近似した方が、より正確に積分値を近似することが出来ます。

ここではより一般的に、積分区間（\(a \le x \le b\)）のN分割を考えます。すると、分割の幅\(\Delta x\)は\(\Delta x =(b - a)/N\)によって定義されます。積分Sを、以下のように各分割区間の積分の和として書き換えてみましょう: \begin{align} S&=\int^{a}_{b} dx f(x) \\ &= \int^{a+\Delta x}_{a} dx f(x)+ \int^{a+2\Delta x}_{a+\Delta x} + \int^{a+3\Delta x}_{a+2\Delta x} dx f(x) + \cdots + \int^{b}_{a+(N-1)\Delta x} dx f(x) \\ &=\sum^{N-1}_{j=0} \int^{a + (j+1)\Delta x}_{a + j\Delta x} dx f(x) \tag{5} \end{align}

分割幅\(\Delta x\)が十分に小さいと仮定すると、被積分関数\(f(x)\)は、各積分区間の両端点の値の平均として近似できます。言い換えると、式(5)は次のように近似できます。 \begin{align} S&=\sum^{N-1}_{j=0} \int^{a + (j+1)\Delta x}_{a + j\Delta x}f(x)dx \nonumber \\ &\approx \sum^{N-1}_{j=0} \int^{a + (j+1)\Delta x}_{a + j\Delta x} \frac{f \left ( a + (j+1)\Delta x \right )+f\left (a + j\Delta x \right )}{2} \nonumber \nonumber \\ &= \sum^{N-1}_{j=0}\frac{f \left ( a + (j+1)\Delta x \right )+f\left (a + j\Delta x \right )}{2} \int^{a + (j+1)\Delta x}_{a + j\Delta x}dx \nonumber \\ &= \sum^{N-1}_{j=0} \frac{f \left ( a + (j+1)\Delta x \right )+f\left (a + j\Delta x \right )}{2} \Delta x \nonumber \\ &= \frac{f(a)}{2}\Delta x + \left [ \sum^{N-1}_{j=1} f(a + j\Delta x) \Delta x \right ] + \frac{f(b)}{2}\Delta x \tag{6} \end{align}

式(6)の近似公式は台形公式または台形則と呼ばれており、この名前は積分値を台形の面積の和として近似することに由来しています。また、式(6)においてN=3とすると、式(3)の3つの台形による積分の近似公式を再現することが確認できます。

この式(6)は、分割数が大きくなる極限(\(N\rightarrow \infty\), \(\Delta x \rightarrow 0\))では、式(3)の台形公式は正確な積分値\(S\)と一致します。

練習として、以下の積分を台形公式を使って評価しましょう。 \begin{align} S=\int^1_0 dx \frac{4}{1+x^2}=\pi . \end{align} 以下は上記の積分を数値的に評価するPythonコードです。数値積分とPythonプログラミングに慣れるために、サンプルコードを参考にして独自のコードで積分を評価してみましょう。

(lesson2_1.py)

 import numpy as np
 
 # define your function
 def my_func(x):
     return 4.0/(1.0+x**2)
 
 # integrate the function from a to b with n points
 def integrate(f,a,b,n):
     h = (b-a)/n
 
     s = (f(a)+f(b))/2.0
     for i in range(1,n):
         x = a + i*h
         s += f(x)
 
     s = s*h
     return s
 
 
 
 a = 0.0
 b = 1.0
 n = 64
 
 num_integral = integrate(my_func,a,b,n)
 
 print('num. integral = ',num_integral)
 print('pi            = ',np.pi)

Lesson 2: 数値積分

Lesson 2-1: 台形公式と数値積分