Lesson 3: 1階微分方程式の求解

Lesson 3-1: オイラー法 (Euler's method)

まず初めに、微分方程式の最も基本的な数値解法としてオイラー法(Euler's method)について学びます。オイラー法を導入するために、Section 1: 数値微分での前進差分公式の議論と同様に、関数の微分について復習してみましょう。関数\(f(x)\)の導関数は次のように定義されます。 \begin{align} y'(x)=\lim_{h\rightarrow 0} \frac{y(x+h)-y(x)}{h}. \tag{2} \end{align} この方程式において\(h\)が十分に小さいと仮定すると、微分は前進差分公式を使用して次のように近似できます。 \begin{align} y'(x)\approx \frac{y(x+h)-y(x)}{h}. \tag{3} \end{align} この方程式を書き換えると、さらに次のように得られます \begin{align} y(x+h)\approx y(x) + y'(x)h. \tag{4} \end{align}

方程式(4)を見ると、右辺は\(x\)での\(y(x)\)と\(y'(x)\)の情報のみで書かれており、この情報のみを使用して関数の\(x+h\)での値\(y(x+h)\)を近似的に評価することができます。したがって、このような操作を順次繰り返すことで、任意の変数\(x\)における関数の値\(y(x)\)を評価することができます。このような微分方程式の数値解法はオイラー法と呼ばれます。以下の図は、オイラー法の手順を図解的に示しています。

以下では、オイラー法の手順をもう少し詳細に説明します。

1. まず、微分方程式(1)の初期条件\(y(x_0)=y_0\)を設定します。
2. 次に、関数\(f(x_0,y(x_0))\)を評価することで、微分値\(y'(x_0)\)を得ます。
3. 式(4)により、評価された微分値\(y'(x_0)\)を使用して、\(x_0+h\)での関数値\(y(x_0+h)\)を評価します。
4. 評価された\(y(x_0+h)\)に基づき、関数値\(f(x_0+h,y(x_0+h))\)を計算し、\(x_0+h\)での微分値\(y'(x_0+h)\)を評価します。
5. 評価された微分値\(y'(x_0+h)\)を使用して、式(4)により\(x_0+2h\)での関数値\(y(x_0+2h)\)を評価します。
6. 以下の同じ手順を繰り返します。

これらの手順に従うことで、微分方程式を数値的に解くことができます。ここで、オイラー法を使用した微分方程式の数値的球解法の練習として、初期条件\(y(x=0)=1\)の下で次の微分方程式を数値的に解いてみましょう： \begin{align} y'(x)=-2x y(x). \tag{5} \end{align} この微分方程式の解はガウス関数、\(y(x)=e^{-x^2}\)であることに注意してください。

以下はPythonコードは、上記の微分方程式(5)を解く計算コードの例です。このコードを参考にして微分方程式を数値的に解くコードを自作し、ステップ幅\(h\)を変更することで得られる解の精度がどのように変化するかを確認してみましょう。

(lesson3_1.py)

 from matplotlib import pyplot as plt
 import numpy as np
 
 # define the derivative, dy/dx
 def dydx(x,y):
     return -2.0*x*y
 
 # Euler method: compute y(x+h)
 def euler_method(y,x,h):
     return y+dydx(x,y)*h
 
 
 # Solve the differential equation from x=a to x=b with n discretized points
 
 a = 0.0
 b = 2.5
 n = 8
     
 h = (b-a)/n
 x_values = np.linspace(a, b, n+1)
 y_values = np.zeros(n+1)
 
 # initial condition, y(a)=y_0
 y_values[0] = 1.0
 
 for i in range(n):
     y_values[i+1] = euler_method(y_values[i],x_values[i],h)
 
 
 # Plot the results
 plt.plot(x_values, y_values, label="Euler method")
 plt.plot(x_values, np.exp(-x_values**2), label="Exact solution", linestyle='dashed')
 
 plt.xlabel('x')
 plt.ylabel('f(x)')
 plt.legend()
 plt.savefig("result_Euler.png")
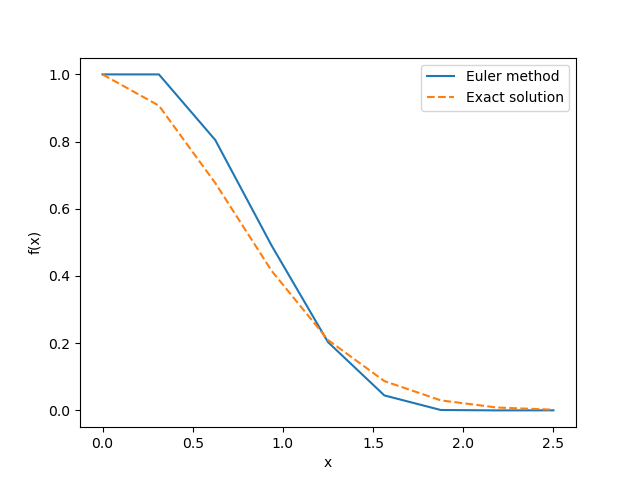
 plt.show()

下の図は、上記のソースコードによって得られた結果を示しています。この計算では、幅\(h\)は2.5/8=0.3125に設定されています。この刻み幅の場合、オイラー法では正確な求解はできず、厳密解から大きな誤差を持っていることが確認できます。

Lesson 3-2: 予測子-修正子法

前の節では、微分方程式を解くための最も単純な方法としてオイラー法について議論しました。しかし、オイラー法は計算精度が低く、計算科学での実際の応用ではあまり使用されません。この節では、より高い精度の解法である予測子-修正子法について説明します。

オイラー法は式(3)の前進差分近似に基づく解法でした。ここでは、より高精度の差分公式として次のような中心差分近似を考えます。 \begin{align} \frac{dy\left ( x+\frac{h}{2} \right )}{dx}\approx \frac{y(x+h)-y(x)}{h} \tag{6} \end{align} さらに、オイラー法の場合と同様に、以下のような書き換えを行います。 \begin{align} y(x+h)\approx y(x)+\frac{dy\left ( x+\frac{h}{2} \right )}{dx}h. \tag{7} \end{align}

ここで、\(x+h/2\)における微分値\( \frac{dy(x+h/2)}{dx} \)を、\(x+h\)と\(x\)での微分値の平均で近似することを考えると、以下の近似式が得られます。 \begin{align} y(x+h)\approx y(x)+h\frac{f\big ( x+h,y(x+h) \big) + f\big ( x,y(x) \big) }{2}. \tag{8} \end{align}

この公式(8)はオイラー法よりも正確な近似式ですが、式(8)の右辺を計算するためには、既に\(x+h\)での関数値\(y(x+h)\)の情報が必要なため、実際の計算で直接使用することは難しいです。式(8)の右辺の\(y(x+h)\)の値を実用的に評価するためには、以下の二段階の手順が使用されます。

まず、手順の最初のステップ（予測ステップ）では、オイラー法を使用して\(x+h\)での\(y(x+h)\)の近似値が以下のように評価します: \begin{align} \bar y (x+h)=y(x)+hf \left (x,y(x)\right). \tag{9} \end{align} ここで、近似値は\(\bar y(x+h) \)と表されます。

二番目のステップ（修正ステップ）では、前のステップで得られた近似値\(\bar y(x+h)\)を使用して、式(7)の右側を評価し、以下のように\(y(x+h)\)を得ます。 \begin{align} y(x+h) = y(x)+h\frac{f\left ( x+h,\bar y(x+h) \right) + f\left ( x,y(x) \right) }{2}. \tag{10} \end{align}

上記の二段階の手順を使用して微分方程式を解く数値的方法は、予測子-修正子法と呼ばれます。オイラー法と予測子-修正子法の精度を比較するために、予測子-修正子法を使用して微分方程式(5)を解き、結果を比較しましょう。

以下のPythonコードは、予測子-修正子法を用いて微分方程式(5)を解くためのサンプルコードです。

(lesson3_2.py)

 from matplotlib import pyplot as plt
 import numpy as np
 
 # define the derivative, dy/dx
 def dydx(x,y):
     return -2.0*x*y
 
 # Predictor-corrector method: compute y(x+h)
 def pred_corr_method(y,x,h):
     y_bar = y+dydx(x,y)*h
     return y+0.5*h*(dydx(x,y)+dydx(x+h,y_bar))
 
 
 # Solve the differential equation from x=a to x=b with n discretized points
 
 a = 0.0
 b = 2.5
 n = 8
     
 h = (b-a)/n
 x_values = np.linspace(a, b, n+1)
 y_values = np.zeros(n+1)
 
 # initial condition, y(a)=y_0
 y_values[0] = 1.0
 
 for i in range(n):
     y_values[i+1] = pred_corr_method(y_values[i],x_values[i],h)
 
 
 # Plot the results
 plt.plot(x_values, y_values, label="Predictor-corrector method")
 plt.plot(x_values, np.exp(-x_values**2), label="Exact solution", linestyle='dashed')
 
 plt.xlabel('x')
 plt.ylabel('f(x)')
 plt.legend()
 plt.savefig("result_PredCorr.png")
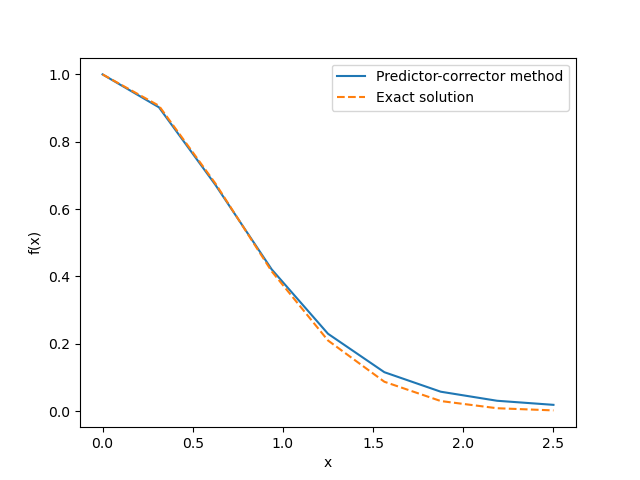
 plt.show()

下の図は、上記の予測子・修正子法のソースコードによって得られた結果を示しています。この計算では、幅\(h\)は2.5/8=0.3125に設定されています

Lesson 3-3 ルンゲ＝クッタ法

ルンゲ＝クッタ法は、常微分方程式の数値解法の一つで、特に4次のルンゲ＝クッタ法（RK4）はその高い精度で広く利用されています。RK4法は、1階常微分方程式 \( \frac{dy}{dx} = f(x, y) \) を以下のようにして解きます。

ルンゲ＝クッタ法の手順は、次のステップに従って、微分方程式の数値解を求めます。

1. 初期条件 \( y(x_0) = y_0 \) を設定します。
2. 微小なステップ幅 \( h \) を選びます。
3. 次の4つの傾きを計算します：
   \[ k_1 = h f(x_n, y_n) \] \[ k_2 = h f(x_n + \frac{h}{2}, y_n + \frac{k_1}{2}) \] \[ k_3 = h f(x_n + \frac{h}{2}, y_n + \frac{k_2}{2}) \] \[ k_4 = h f(x_n + h, y_n + k_3) \]
4. 次の点での値を計算します：
   \[ y_{n+1} = y_n + \frac{1}{6} (k_1 + 2k_2 + 2k_3 + k_4) \]
5. \( x \) を \( x + h \) に更新し、3. からの手順を繰り返します。

以下のPythonコードは、ルンゲ＝クッタ法を使用して1階常微分方程式を解く例です。具体的には、微分方程式 \( y'(x) = -2xy \) を解きます。

from matplotlib import pyplot as plt
import numpy as np

# define the derivative, dy/dx
def dydx(x, y):
    return -2.0 * x * y

# Runge-Kutta method of 4th order
def runge_kutta(y, x, h):
    k1 = h * dydx(x, y)
    k2 = h * dydx(x + 0.5 * h, y + 0.5 * k1)
    k3 = h * dydx(x + 0.5 * h, y + 0.5 * k2)
    k4 = h * dydx(x + h, y + k3)
    return y + (k1 + 2 * k2 + 2 * k3 + k4) / 6

# Solve the differential equation from x=a to x=b with n discretized points
a = 0.0
b = 2.5
n = 8

h = (b - a) / n
x_values = np.linspace(a, b, n + 1)
y_values = np.zeros(n + 1)

# initial condition, y(a) = y_0
y_values[0] = 1.0

for i in range(n):
    y_values[i + 1] = runge_kutta(y_values[i], x_values[i], h)

# Plot the results
plt.plot(x_values, y_values, label="Runge-Kutta method")
plt.plot(x_values, np.exp(-x_values ** 2), label="Exact solution", linestyle='dashed')

plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.savefig("result_RK4.png")
plt.show()

上記のPythonコードを実行すると、ルンゲ＝クッタ法による数値解と、関数 \( y(x) = e^{-x^2} \) による正確な解を比較することができます。結果として得られるプロットから、ルンゲ＝クッタ法が高い精度で微分方程式を解くことが確認できます。